
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
| 2 |

| 2 |
| 2 |
| y2-y1 |
| x2-x1 |
| 2 |
| 2 |
| 2 |
| x2 |
| 8 |
| y2 |
| 4 |
| x2 |
| 4 |
| y2 |
| 4 |
| y |
| x+2 |
| y |
| x-2 |
| y2 |
| x2-4 |
| x2 |
| 4 |
| y2 |
| 4 |
|
| -8k12 |
| 2k12+1 |
| 8k12-8 |
| 2k12+1 |
| 1+k12 |
| (x1+x2)2-4x1x2 |
4
| ||
| 2k12+1 |
| 1+k22 |
| (x1+x2)2-4x1x2 |
4
| ||
| 2k22+1 |
| 1 |
| k1 |
4
| ||
| k12+2 |
| 1 |
| |AB| |
| 1 |
| |CD| |
3
| ||
| 8 |
3
| ||
| 8 |
| x2 |
| 4 |
| y2 |
| 4 |



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| 3 |
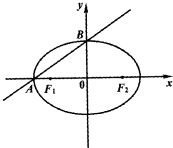
| MC |
| CN |
| MD |
| DN |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
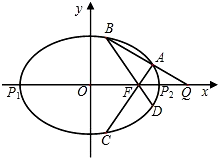 ��2013•������ģ����ͼ����֪��ԲE��
��2013•������ģ����ͼ����֪��ԲE��| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| 1 |
| |P1Q| |
| 1 |
| |P2Q| |
| 2 |
| |FQ| |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2013-2014ѧ�갲��ʡ�����и�����ѧ����ĩ����������ѧ�Ծ��������棩 ���ͣ������
��ͼ����֪��ԲE��������ԭ��O�����ҽ���ΪF(2��0)����x����һ��A(3,0)��ֱ�� ����ԲE�ཻ��P,Q����,��
����ԲE�ཻ��P,Q����,�� �����ֵΪ
�����ֵΪ .
.

(��)����ԲE�ķ���;
(��)�� ,����P��ƽ����y���ֱ������ԲE�ཻ����һ��M,����M,F,Q�Ƿ��ߣ���������֤������֮˵������.
,����P��ƽ����y���ֱ������ԲE�ཻ����һ��M,����M,F,Q�Ƿ��ߣ���������֤������֮˵������.
�鿴�𰸺ͽ���>>
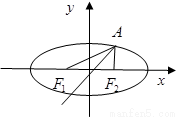
��Ŀ��������ѧ ��Դ��2013�켪��ʡ�߶����п����Ŀ���ѧ�Ծ��������棩 ���ͣ������
��ͼ����֪��ԲE������A��2,3�����Գ���Ϊ�����ᣬ���� ��
�� ��x���ϣ�������
��x���ϣ�������
��1������ԲE�ķ��̣�
��2����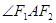 �Ľ�ƽ��������ֱ��
�Ľ�ƽ��������ֱ�� �ķ���.
�ķ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2013���㽭ʡ�����и߿���ѧ��ģ�Ծ������ƣ��������棩 ���ͣ������
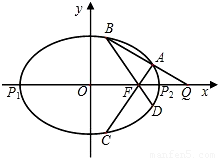
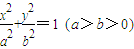 ����������
����������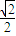 ��P1��P2����ԲE�ij���������˵㣨P2λ��P1�Ҳࣩ����F����ԲE���ҽ��㣮��Q��x����λ��P2�Ҳ��һ�㣬������
��P1��P2����ԲE�ij���������˵㣨P2λ��P1�Ҳࣩ����F����ԲE���ҽ��㣮��Q��x����λ��P2�Ҳ��һ�㣬������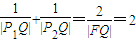 ��
��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com