
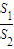 = .
= .  a,从而得到S2关于a的式子.利用正三角形面积公式,算出正四面体的表面积S1关于a的式子,由此不难得出S1与S2的比值.
a,从而得到S2关于a的式子.利用正三角形面积公式,算出正四面体的表面积S1关于a的式子,由此不难得出S1与S2的比值.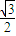 a,底面中心将高分为2:1的两段
a,底面中心将高分为2:1的两段 ×
×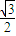 a=
a=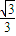 a
a =
= a
a ×S△ABC×
×S△ABC×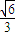 a=
a= a2,
a2, ×S△ABC×r=
×S△ABC×r=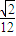 a2,解得r=
a2,解得r=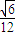 a
a
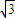 a2,
a2,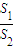 =
=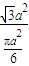 =
=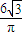
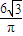


 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:
 设棋子在正四面体ABCD的表面从一个顶点移向另外三个顶点是等可能的,现投掷骰子根据其点数决定棋子是否移动:若投出的点数是偶数,棋子移动到另一个顶点;若投出的点数是奇数,则棋子不动.若棋子的初始位置在顶点A.
设棋子在正四面体ABCD的表面从一个顶点移向另外三个顶点是等可能的,现投掷骰子根据其点数决定棋子是否移动:若投出的点数是偶数,棋子移动到另一个顶点;若投出的点数是奇数,则棋子不动.若棋子的初始位置在顶点A.查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2010年孝感高中高一下学期期末考试数学卷 题型:解答题
(本小题满分12分)
 设棋子在正四面体ABCD的表面从一个顶点移向另外三个顶点是等可能的,现投掷骰子根据其点数决定棋子是否移动:若投出的点数是偶数,棋子移动到另一个顶点;若投出的点数是奇数,则棋子不动.若棋子的初始位置在顶点A.
设棋子在正四面体ABCD的表面从一个顶点移向另外三个顶点是等可能的,现投掷骰子根据其点数决定棋子是否移动:若投出的点数是偶数,棋子移动到另一个顶点;若投出的点数是奇数,则棋子不动.若棋子的初始位置在顶点A.
求:(Ⅰ)投了2次骰子,棋子才到达顶点B的概率;
(Ⅱ)记投了n次骰子,棋子在顶点B的概率为 .求
.求 .
.
查看答案和解析>>
科目:高中数学 来源:2010年孝感高中高一下学期期末考试数学卷 题型:解答题
(本小题满分12分)
 设棋子在正四面体ABCD的表面从一个顶点移向另外三个顶点是等可能的,现投掷骰子根据其点数决定棋子是否移动:若投出的点数是偶数,棋子移动到另一个顶点;若投出的点数是奇数,则棋子不动.若棋子的初始位置在顶点A.
设棋子在正四面体ABCD的表面从一个顶点移向另外三个顶点是等可能的,现投掷骰子根据其点数决定棋子是否移动:若投出的点数是偶数,棋子移动到另一个顶点;若投出的点数是奇数,则棋子不动.若棋子的初始位置在顶点A.
求:(Ⅰ)投了2次骰子,棋子才到达顶点B的概率;
(Ⅱ)记投了n次骰子,棋子在顶点B的概率为 .求
.求 .
.
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com