练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    在研究色盲与性别的关系调查中，调查了男性480人，其中有38人患色盲，调查的520个女性中6人患色盲，
    （1）根据以上的数据建立一个2×2的列联表；
    （2）若认为“性别与患色盲有关系”，则出错的概率会是多少
    （本题可以参考两个分类变量x和y有关系的可信度表:）
    （1）
     
    		患色盲
    		不患色盲
    		总计
    男
    		38
    		442
    		480
    女
    		6
    		514
    		520
    总计
    		44
    		956
    		1000
    （2）出错的概率为0.001

    试题分析：解：（1）
     
    		患色盲
    		不患色盲
    		总计
    男
    		38
    		442
    		480
    女
    		6
    		514
    		520
    总计
    		44
    		956
    		1000
    （2）假设H ：“性别与患色盲没有关系”先算出K 的观测值：

    则有
    即是H 成立的概率不超过0.001,
    若认为“性别与患色盲有关系”，则出错的概率为0.001
    点评：主要是考查了独立性检验的思想的运用，属于基础题。
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：不详 题型：填空题

    为了解篮球爱好者小李的投篮命中率与打篮球时间之间的关系,下表记录了小李某月1号到5号每天打篮球时间x(单位:小时)与当天投篮命中率y之间的关系:
    时间x
    		1
    		2
    		3
    		4
    		5
    命中率y
    		0.4
    		0.5
    		0.6
    		0.6
    		0.4
    小李这5天的平均投篮命中率为　　　　;用线性回归分析的方法,预测小李该月6号打6小时篮球的投篮命中率为　　　　.

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    利用独立性检验来判断两个分类变量X和Y是否有关系，通过查阅下表来确定“X和Y有关系”的可信度.为了调查用电脑时间与视力下降是否有关系，现从某地网民中抽取100位居民进行调查.经过计算得，那么就有_______________%的根据认为用电脑时间与视力下降有关系.

    		0.50
    		0.40
    		0.25
    		0.15
    		0.10
    		0.05
    		0.025
    		0.010
    		0.005
    		0.001

    		0.455
    		0.708
    		1.323
    		2.072
    		2.706
    		3.841
    		5.024
    		6.635
    		7.879
    		10.828

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    给出施化肥量（kg）对水稻产量（kg）影响的试验数据：
    施化肥量x
    		15
    		20
    		25
    		30
    水稻产量y
    		330
    		345
    		365
    		405
    （1）试求出回归直线方程；
    （2）请估计当施化肥量为10时，水稻产量为多少？
    （已知：7.5×31.25+2.5×16.25+2.5×3.75+7.5×43.75=612.5,2×7.5×7.5+2×2.5×2.5=125）

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    已知、之间的一组数据如右表：

    		0
    		1
    		2
    		3

    		8
    		2
    		6
    		4
    则线性回归方程所表示的直线必经过点 (       )
    A．（0，0）         B．（1.5,5）         C．（4,1.5）          D．（2,2）

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    2012年元旦、春节前夕，各个物流公司都出现了爆仓现象，直接原因就是网上疯狂的购物．某商家针对人们在网上购物的态度在某城市进行了一次调查，共调查了124人，其中女性70人，男性54人．女性中有43人对网上购物持赞成态度，另外27人持反对态度；男性中有21人赞成网上购物，另外33人持反对态度．
    (Ⅰ) 估计该地区对网上购物持赞成态度的比例；
    (Ⅱ) 有多大的把握认为该地区对网上购物持赞成态度与性别有关；
    附：表1

    K2＝

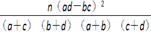
    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    对变量与,分别选择了4个不同的回归方程甲、乙、丙、丁,它们的相关系数分别为: ，, , . 其中拟合效果最好的是方程（    ）.
    A．甲B．乙C．丙D．丁

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

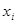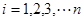    对于一组数据()，如果将它们改变为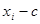(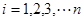)，其中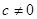，下列结论正确的是(   )
    A．平均数与方差均不变B．平均数变了，而方差保持不变
    C．平均数不变，而方差变了D．平均数与方差均发生了变化

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

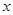    假设关于某设备的使用年限和所支出的维修费用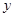(万元)统计数据如下:
    使用年限x
    		2
    		3
    		4
    		5
    		6
    维修费用y
    		2.2
    		3.8
    		5.5
    		6.5
    		7.0
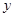    若有数据知对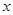呈线性相关关系.求:
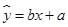    (1) 求出线性回归方程的回归系数；
    (2) 估计使用10年时,维修费用是多少。

    查看答案和解析>>

    同步练习册答案