
【题目】如图,梯形![]() 中,
中,![]() 且
且![]() ,沿
,沿![]() 将梯形
将梯形![]() 折起,使得平面
折起,使得平面![]() ⊥平面
⊥平面![]()
![]() .
.
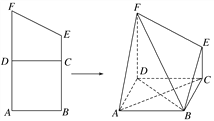
(1)证明:![]() ;
;
(2)求三棱锥![]() 的体积;
的体积;
(3)求直线![]() 。
。
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】试题分析:(1)取BF中点为M,AC与BD交点为O,连结MO,ME,由已知结合三角形中位线定理可得四边形OCEM为平行四边形,然后利用线面平行的判定得答案;
(2)由线面垂直的性质定理可得BC⊥平面DEF,然后把三棱锥D-BEF的体积转化为三棱锥B-DEF的体积求解.
(3)分析条件得![]() ,连结
,连结![]() ,
,![]() ,由
,由![]() 求解即可.
求解即可.
试题解析:
(1)证明 如图,取BF的中点![]() ,设
,设![]() 与
与![]() 交点为
交点为![]() ,连接
,连接![]() .
.
由题设知,![]() ,
,
∴![]() ,故四边形
,故四边形![]() 为平行四边形,
为平行四边形,
![]() 即
即![]() .
.
又![]() ,
,![]() ,
,
∴![]() .
.
(2)解 ∵平面![]() ⊥平面
⊥平面![]() ,平面
,平面![]() ∩平面
∩平面![]() =
=![]() ,
,![]() ⊥
⊥![]() ,
,
∴![]() ⊥平面
⊥平面![]() .
.
∴三棱锥![]() 的体积为
的体积为
![]() .
.
(3)∵平面![]() ⊥平面
⊥平面![]() ,平面
,平面![]() ∩平面
∩平面![]() =
=![]() ,又
,又![]()
![]() 又
又![]() ,
,
![]()
又在正方形![]() 中
中
![]()
![]()
连结![]() ,
,![]()
![]()
![]()
![]()
![]()


科目:高中数学 来源: 题型:
【题目】2009年推出一种新型家用轿车,购买时费用为![]() 万元,每年应交付保险费、养路费及汽油费共
万元,每年应交付保险费、养路费及汽油费共![]() 万元,汽车的维修费为:第一年无维修费用,第二年为
万元,汽车的维修费为:第一年无维修费用,第二年为![]() 万元,从第三年起,每年的维修费均比上一年增加
万元,从第三年起,每年的维修费均比上一年增加![]() 万元.
万元.
(1)设该辆轿车使用![]() 年的总费用(包括购买费用、保险费、养路费、汽油费及维修费)为
年的总费用(包括购买费用、保险费、养路费、汽油费及维修费)为![]() ,求
,求![]() 的表达式;
的表达式;
(2)这种汽车使用多少年报废最合算(即该车使用多少年,年平均费用最少)?
查看答案和解析>>
科目:高中数学 来源: 题型:
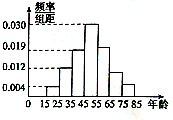
【题目】某购物中心为了了解顾客使用新推出的某购物卡的顾客的年龄分布情况,随机调查了![]() 位到购物中心购物的顾客年龄,并整理后画出频率分布直方图如图所示,年龄落在区间
位到购物中心购物的顾客年龄,并整理后画出频率分布直方图如图所示,年龄落在区间![]() 内的频率之比为
内的频率之比为![]() .
.
(1) 求顾客年龄值落在区间![]() 内的频率;
内的频率;
(2) 拟利用分层抽样从年龄在![]() 的顾客中选取
的顾客中选取![]() 人召开一个座谈会,现从这
人召开一个座谈会,现从这![]() 人中选出
人中选出![]() 人,求这两人在不同年龄组的概率.
人,求这两人在不同年龄组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随机抽取某中学甲、乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图7.

(1)根据茎叶图判断哪个班的平均身高较高;
(2)计算甲班的样本方差;
(3)现从乙班这10名同学中随机抽取两名身高不低于173cm的同学,求身高为176cm的同学被抽中的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位每天的用电量![]() (度)与当天最高气温
(度)与当天最高气温![]() (℃)之间具有线性相关关系,下表是该单位随机统计4天的用电量与当天最高气温的数据.
(℃)之间具有线性相关关系,下表是该单位随机统计4天的用电量与当天最高气温的数据.
最高气温(℃) | 26 | 29 | 31 | 34 |
用电量 (度) | 22 | 26 | 34 | 38 |
(Ⅰ)根据表中数据,求出回归直线的方程![]() (其中
(其中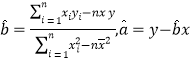 );
);
(Ⅱ)试预测某天最高气温为33℃时,该单位当天的用电量(精确到1度).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin![]() -2
-2![]() ·sin2x.
·sin2x.
(1) 求函数f(x)的最小正周期;
(2) 求函数f(x)图象的对称轴方程、对称中心的坐标;
(3) 当0≤x≤![]() 时,求函数f(x)的最大、最小值.
时,求函数f(x)的最大、最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={1,2,3,4,5,6,7,8,9),在集合A中任取三个元素,分别作为一个三位数的个位数,十位数和百位数,记这个三位数为a,现将组成a的三个数字按从小到大排成的三位数记为I(a),按从大到小排成的三位数记为D(a)(例如a=219,则I(a)=129,D(a)=921),阅读如图所示的程序框图,运行相应的程序,任意输入一个a,则输出b的值为( )
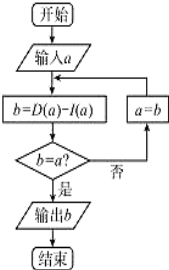
A.792 B.693
C.594 D.495
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com