
【题目】已知函数f(x)=sin![]() -2
-2![]() ·sin2x.
·sin2x.
(1) 求函数f(x)的最小正周期;
(2) 求函数f(x)图象的对称轴方程、对称中心的坐标;
(3) 当0≤x≤![]() 时,求函数f(x)的最大、最小值.
时,求函数f(x)的最大、最小值.
【答案】(1)![]() (2)对称轴方程是
(2)对称轴方程是![]() ,对称中心的坐标是
,对称中心的坐标是![]() (3)最小值
(3)最小值![]() ,最大值为
,最大值为![]()
【解析】试题分析(1)先根据两角差正弦公式、二倍角公式以及配角公式将函数化为基本三角函数,再利用正弦函数性质求周期(2)根据正弦函数性质求对称轴方程、对称中心的坐标(3)先求![]() 范围,再利用正弦函数性质求最值
范围,再利用正弦函数性质求最值
试题解析:解:f(x)=![]() sin 2x-
sin 2x-![]() cos 2x-2
cos 2x-2![]() ·
·![]() =
=![]() sin 2x+
sin 2x+![]() cos 2x-
cos 2x-![]() =sin
=sin![]() -
-![]() .
.
(1) 函数f(x)的最小正周期为π.
(2) 令2x+![]() =kπ+
=kπ+![]() (k∈Z),得x=
(k∈Z),得x=![]() kπ+
kπ+![]() ,所以函数f(x)图象的对称轴方程是x=
,所以函数f(x)图象的对称轴方程是x=![]() kπ+
kπ+![]() (k∈Z).
(k∈Z).
令2x+![]() =kπ(k∈Z),得x=
=kπ(k∈Z),得x=![]() kπ-
kπ-![]() ,所以函数f(x)图象的对称中心的坐标是(
,所以函数f(x)图象的对称中心的坐标是(![]() kπ-
kπ-![]() ,-
,-![]() )(k∈Z).
)(k∈Z).
(3) 当0≤x≤![]() 时,
时,![]() ≤2x+
≤2x+![]() ≤
≤![]() ,-
,-![]() ≤sin
≤sin![]() ≤1,所以当x=
≤1,所以当x=![]() 时,f(x)取最小值-
时,f(x)取最小值-![]() ,当x=
,当x=![]() 时,f(x)取最大值为1-
时,f(x)取最大值为1-![]()


科目:高中数学 来源: 题型:
【题目】某高科技企业生产产品![]() 和产品
和产品![]() 需要甲、乙两种新型材料,生产一件产品
需要甲、乙两种新型材料,生产一件产品![]() 需要甲材料1.5
需要甲材料1.5![]() ,乙材料1
,乙材料1![]() ,用5个工时,生产一件产品需要甲材料0.5
,用5个工时,生产一件产品需要甲材料0.5![]() ,乙材料0.3
,乙材料0.3![]() ,用3个工时,生产一件产品的利润为2100元,生产一件产品的利润为900元.该企业现有甲材料150
,用3个工时,生产一件产品的利润为2100元,生产一件产品的利润为900元.该企业现有甲材料150![]() ,乙材料90
,乙材料90![]() ,则在不超过600个工时的条件下,生产产品
,则在不超过600个工时的条件下,生产产品![]() 的利润之和的最大值为____________元.
的利润之和的最大值为____________元.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.
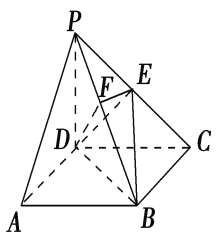
(1)求证:PA∥平面EDB;
(2)求证:PB⊥平面EFD;
(3)求二面角C-PB-D的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() ,
,![]() .设
.设![]() 分别为
分别为![]() 中点.
中点.
(1)求证:![]() 平面
平面![]() ;
;
(2)求证:![]() 平面
平面![]() ;
;
(3)试问在线段![]() 上是否存在点
上是否存在点![]() ,使得过三点
,使得过三点![]() 的平面内的任一条直线都与平面
的平面内的任一条直线都与平面![]() 平行?
平行?
若存在,指出点![]() 的位置并证明;若不存在,请说明理由.
的位置并证明;若不存在,请说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量a=(cos α,sin α),b=(cos β,sin β),c=(-1,0).
(1) 求向量b+c的模的最大值;
(2) 若α=![]() ,且a⊥(b+c),求cos β的值.
,且a⊥(b+c),求cos β的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知圆C1:(x+3)2+(y-1)2=4和圆C2:(x-4)2+(y-5)2=4.若直线l过点A(4,0),且被圆C1截得的弦长为2![]() ,求直线l的方程;
,求直线l的方程;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2015年10月十八届五中全会决定2016年1月1日起全国统一实施全面两孩政策,为了了解适龄民众对放开生育二胎政策的态度,某市进行了一次民意调查,参与调查的100位市民中,年龄分布情况如下图所示,并得到适龄民众对放开生育二胎政策的态度数据如下表:
生二胎 | 不生二胎 | 合计 | |
25~35岁 | 10 | ||
35~50岁 | 30 | ||
合计 | 100 |
(1)填写上面的![]() 列联表;
列联表;
(2)根据调查数据,有多少的把握认为“生二胎与年龄有关”,说明理由;
(3)调查对象中决定生二胎的民众有六人分别来自三个不同的家庭且为父子,各自家庭都有一个约定:父亲先生二胎,然后儿子生二胎,则这三个家庭“二胎出生的日期的先后顺序”有多少种?
参考数据:
| 0.15 | 0.10 | 0.05 | 0.010 |
| 2.072 | 2.706 | 3.841 | 6.635 |
(参考公式:![]() ,其中
,其中![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com