
【题目】2015年10月十八届五中全会决定2016年1月1日起全国统一实施全面两孩政策,为了了解适龄民众对放开生育二胎政策的态度,某市进行了一次民意调查,参与调查的100位市民中,年龄分布情况如下图所示,并得到适龄民众对放开生育二胎政策的态度数据如下表:
生二胎 | 不生二胎 | 合计 | |
25~35岁 | 10 | ||
35~50岁 | 30 | ||
合计 | 100 |
(1)填写上面的![]() 列联表;
列联表;
(2)根据调查数据,有多少的把握认为“生二胎与年龄有关”,说明理由;
(3)调查对象中决定生二胎的民众有六人分别来自三个不同的家庭且为父子,各自家庭都有一个约定:父亲先生二胎,然后儿子生二胎,则这三个家庭“二胎出生的日期的先后顺序”有多少种?
参考数据:
| 0.15 | 0.10 | 0.05 | 0.010 |
| 2.072 | 2.706 | 3.841 | 6.635 |
(参考公式:![]() ,其中
,其中![]() )
)
【答案】(1)见解析;(2)有90% 以上的把握认为“生二胎与年龄有关”;(3)![]() .
.
【解析】
试题分析:(1)根据题意,填写![]() 列联表即可;
列联表即可;
(2)根据调查数据计算![]() ,对照数表即可得出结论;
,对照数表即可得出结论;
(3)分别计算三对父子的二胎出生日期仅为不同的二天、不同的三天、不同的四天、不同的五天和不同的六天时的种数,求和即可.
试题解析:
解:(1)
| 生二胎 | 不生二胎 | 合计 |
25~35岁 | (45) | 10 | (55) |
35~50岁 | 30 | (15) | (45) |
合计 | (75) | (25) | 100 |
-------3分
(2)![]() -7分
-7分
所以有90% 以上的把握认为“生二胎与年龄有关”-------------8分
(3)(以前的答案有误)三对父子的二胎出生日期仅为不同的二天,则有1种;
三对父子的二胎出生日期仅为不的三天,则有![]() 种; --------9分
种; --------9分
三对父子的二胎出生日期仅为不同的四天,则有![]() 种;10分
种;10分
三对父子的二胎出生日期仅为不同的五天,则有
![]() 种; --------11分
种; --------11分
三对父子的二胎出生日期仅为不同的六天,则有
![]() 或
或![]() 种.
种.
故共计![]() 种 ----12分
种 ----12分
(后四种每写对一种得1分)


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin![]() -2
-2![]() ·sin2x.
·sin2x.
(1) 求函数f(x)的最小正周期;
(2) 求函数f(x)图象的对称轴方程、对称中心的坐标;
(3) 当0≤x≤![]() 时,求函数f(x)的最大、最小值.
时,求函数f(x)的最大、最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={1,2,3,4,5,6,7,8,9),在集合A中任取三个元素,分别作为一个三位数的个位数,十位数和百位数,记这个三位数为a,现将组成a的三个数字按从小到大排成的三位数记为I(a),按从大到小排成的三位数记为D(a)(例如a=219,则I(a)=129,D(a)=921),阅读如图所示的程序框图,运行相应的程序,任意输入一个a,则输出b的值为( )
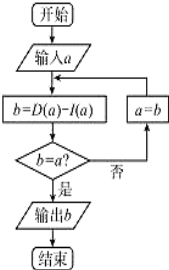
A.792 B.693
C.594 D.495
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 的离心率为
的离心率为![]() ,点
,点![]() 在椭圆C上.
在椭圆C上.
(1)求椭圆C的方程;
(2)设动直线![]() 与椭圆C有且仅有一个公共点,判断是否存在以原点O为圆心的圆,满足此圆与
与椭圆C有且仅有一个公共点,判断是否存在以原点O为圆心的圆,满足此圆与![]() 相交两点
相交两点![]() ,
,![]() (两点均不在坐标轴上),且使得直线
(两点均不在坐标轴上),且使得直线![]() ,
,![]() 的斜率之积为定值?若存在,求此圆的方程;若不存在,说明理由.
的斜率之积为定值?若存在,求此圆的方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业开发一种新产品,现准备投入适当的广告费,对产品进行促销,在一年内,预计年销量Q(万件)与广告费x(万件)之间的函数关系为![]() ,已知生产此产品的年固定投入为3万元,每年产1万件此产品仍需要投入32万元,若年销售额为
,已知生产此产品的年固定投入为3万元,每年产1万件此产品仍需要投入32万元,若年销售额为![]() ,而当年产销量相等。
,而当年产销量相等。
(1)试将年利润P(万件)表示为年广告费x(万元)的函数;
(2)当年广告费投入多少万元时,企业年利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,椭圆短轴的一个端点与两个焦点构成的三角形的面积为
,椭圆短轴的一个端点与两个焦点构成的三角形的面积为![]() .
.
(1)求椭圆![]() 的方程式;
的方程式;
(2)已知动直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点.
两点.
①若线段![]() 中点的横坐标为
中点的横坐标为![]() ,求斜率
,求斜率![]() 的值;
的值;
②已知点![]() ,求证:
,求证:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市政府为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准![]() (吨),一位居民的月用水量不超过
(吨),一位居民的月用水量不超过![]() 的部分按平价收费,超出
的部分按平价收费,超出![]() 的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照
的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照![]() ,…,
,…,![]() 分成9组,制成了如图所示的频率分布直方图.
分成9组,制成了如图所示的频率分布直方图.
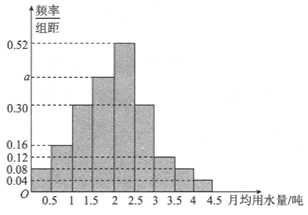
(1)求直方图中![]() 的值;
的值;
(2)若该市有110万居民,估计全市居民中月均用水量不低于3吨的人数,请说明理由;
(3)估计居民月均用水量的中位数(精确到0.01)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中常数
,其中常数![]() .
.
(1)当![]() ,求函数
,求函数![]() 的单调递增区间;
的单调递增区间;
(2)设定义在![]() 上的函数
上的函数![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,若
,若![]() 在
在![]() 内恒成立,则称
内恒成立,则称![]() 为函数
为函数![]() 的“类对称点”,当
的“类对称点”,当![]() 时,试问
时,试问![]() 是否存在“类对称点”,若存在,请至少求出一个“类对称点”的横坐标;若不存在,请说明理由.
是否存在“类对称点”,若存在,请至少求出一个“类对称点”的横坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com