
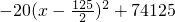 ,(0≤x≤100,x∈N)
,(0≤x≤100,x∈N)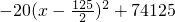 ,(0≤x≤100,x∈N),由此能求出最大利润和取得最大利润时的产量.
,(0≤x≤100,x∈N),由此能求出最大利润和取得最大利润时的产量.

科目:高中数学 来源: 题型:单选题
 =(1,2),
=(1,2), =(x,2),则向量
=(x,2),则向量 +2
+2 与2
与2 -
-
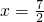
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
 ,n为正整数,则使 Tn最大的n的值为
,n为正整数,则使 Tn最大的n的值为 查看答案和解析>>
科目:高中数学 来源: 题型:解答题
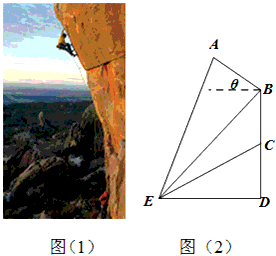 攀岩运动是一项刺激而危险的运动,如图(1)在某次攀岩活动中,两名运动员在如图所在位置,为确保运动员的安全,地面救援者应时刻注意两人离地面的距离,以备发生危险时进行及时救援.为了方便测量和计算,现如图(2)A,C分别为两名攀岩者所在位置,B为山的拐角处,且斜坡AB的坡角为θ,D为山脚,某人在E处测得A,B,C的仰角分别为α,β,γ,ED=α,求:
攀岩运动是一项刺激而危险的运动,如图(1)在某次攀岩活动中,两名运动员在如图所在位置,为确保运动员的安全,地面救援者应时刻注意两人离地面的距离,以备发生危险时进行及时救援.为了方便测量和计算,现如图(2)A,C分别为两名攀岩者所在位置,B为山的拐角处,且斜坡AB的坡角为θ,D为山脚,某人在E处测得A,B,C的仰角分别为α,β,γ,ED=α,求:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
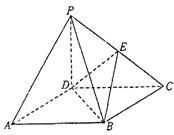 如图,四棱锥P-ABCD的底面ABCD是正方形,
如图,四棱锥P-ABCD的底面ABCD是正方形,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
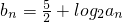 ,求数列{bn}的前n项和Tn
,求数列{bn}的前n项和Tn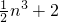 (n=1,2,3…)的大小,并说明理由.
(n=1,2,3…)的大小,并说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com