
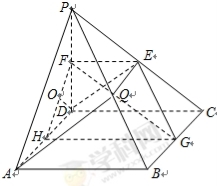
如图,在四棱锥 中,
中, 是正方形,
是正方形, 平面
平面 ,
, ,
, 分别是
分别是 的中点.
的中点.

(1)在线段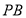 上确定一点
上确定一点 ,使
,使 平面
平面 ,并给出证明;
,并给出证明;
(2)证明平面 平面
平面 ,并求出
,并求出 到平面
到平面 的距离.
的距离.
(1)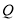 为线段
为线段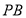 中点时,
中点时,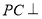 平面
平面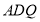 ;(2)
;(2)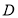 到
到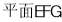 的距离为
的距离为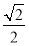 .
.
【解析】
试题分析:
(1)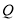 为线段
为线段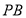 中点,连接
中点,连接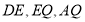 ,可得出
,可得出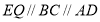 ,所以
,所以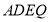 为平面四边形,先证
为平面四边形,先证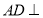 平面
平面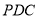 ,所以
,所以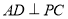 ,又三角形
,又三角形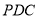 为等腰直角三角形,
为等腰直角三角形,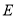 为斜边中点,所以
为斜边中点,所以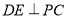 .即可得结论
.即可得结论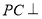 平面
平面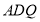 ;
;
(2)根据线线垂直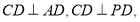 可得线面垂直
可得线面垂直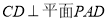 ,
,
进而推出面面垂直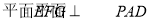 .
.
取所以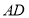 中点所以
中点所以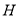 ,证明
,证明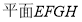 即为
即为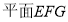 ,因为
,因为  ,在平面
,在平面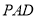 内,作
内,作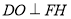 ,垂足为
,垂足为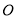 ,则
,则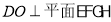 ,
, 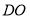 即为
即为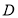 到
到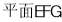 的距离,在三角形
的距离,在三角形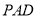 中,
中,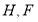 为
为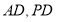 中点,
中点,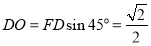 ,即
,即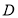 到
到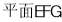 的距离为
的距离为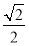 (12分)
(12分)
试题解析:(1) 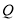 为线段
为线段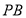 中点时,
中点时,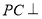 平面
平面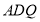 .
.
取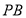 中点
中点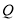 ,连接
,连接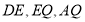 ,
,
由于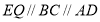 ,所以
,所以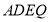 为平面四边形,
为平面四边形,
由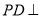 平面
平面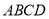 ,得
,得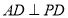 ,
,
又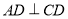 ,
,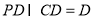 ,所以
,所以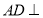 平面
平面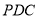 ,
,
所以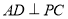 ,
,
又三角形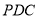 为等腰直角三角形,
为等腰直角三角形,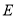 为斜边中点,所以
为斜边中点,所以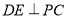 ,
,
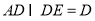 ,所以
,所以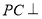 平面
平面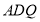 . (5分)
. (5分)
(2)因为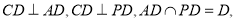 所以
所以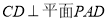 .
.
又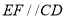 ,所以
,所以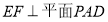 ,所以
,所以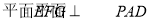 .
.
取所以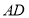 中点所以
中点所以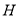 ,连接所以
,连接所以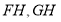 ,则
,则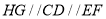 ,
,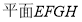 即为
即为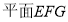 ,
,
在平面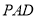 内,作
内,作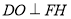 ,垂足为
,垂足为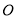 ,则
,则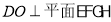 ,
,
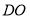 即为
即为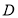 到
到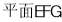 的距离,
的距离,
在三角形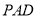 中,
中,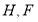 为
为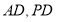 中点,
中点,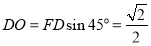 ,
,
即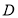 到
到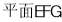 的距离为
的距离为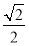 (12分)
(12分)
考点:本题考查线线、线面垂直的判断和性质,可通过线线垂直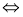 线面垂直
线面垂直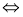 面面垂直的等价转化方法;
面面垂直的等价转化方法;
点到平面的距离,可先做垂线,在解三角形.


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:高中数学 来源:2016届福建省高一上学期期末数学试卷(解析版) 题型:填空题
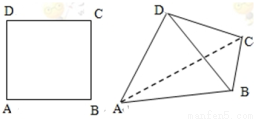
如图,将边长为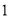 的正方形
的正方形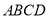 沿对角线
沿对角线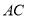 折起,使得平面
折起,使得平面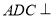 平面
平面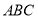 ,在折起后形成的三棱锥
,在折起后形成的三棱锥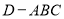 中,给出下列三个命题:
中,给出下列三个命题:
①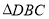 是等边三角形;②
是等边三角形;②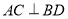 ;③三棱锥
;③三棱锥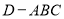 的体积是
的体积是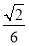 ;④AB与CD所成的角是60°。其中正确命题的序号是 .(写出所有正确命题的序号)
;④AB与CD所成的角是60°。其中正确命题的序号是 .(写出所有正确命题的序号)
查看答案和解析>>
科目:高中数学 来源:2016届甘肃天水一中高一上学期必修一第一学段考试数学试卷(解析版) 题型:填空题
某种商品进货价每件50元,据市场调查,当销售价格(每件x元)在 时,每天售出的件数
时,每天售出的件数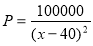 ,当销售价格定为 元时所获利润最多.
,当销售价格定为 元时所获利润最多.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com