Question

下列四个命题：
①m=是两直线2x+my十1=0与mx+y-1=0平行的充分必要条件；②直线y=kx与圆（x-cosθ）²+（y-sinθ）²=1恒有公共点．③当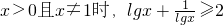；④一椭圆内切于长为6，宽为2的矩形，在矩形内随机地撒300颗黄豆，数得落在椭圆外的黄豆数为96颗，以此实验数据为依据可以估算出椭圆的面积约为 8.16．正确命题的序号为________ （写出所有正确命题的序号）

Answer 1

②④
分析：①把m=代入两方程，根据两直线平行的条件得到两直线平行；而当两直线平行时，根据两直线平行时所满足的条件得到m=±，进而得到本选项为假命题；
②观察圆的方程发现，此圆为圆心为原点的单位圆，而直线为过原点的直线，所以两者横有公共点，本选项为真命题；
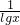③当x大于0小于1时，lgx小于0，利用基本不等式得到lgx+的最小值为-2，本选项为假命题；
④根据模拟方法来估算黄豆数的概率，利用实验得到的频率估算出概率，然后根据面积之比等于概率之比，即可求出椭圆的面积为8.16，本命题为真命题．
解答：①把m=，代入得：
两直线方程为2x+y十1=0与x+y-1=0，
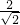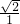由=，-1≠1，得到两直线平行；
而两直线平行时，由两直线2x+my十1=0与mx+y-1=0，
得到=，即m²=2，解得m=或m=-，
所以m=是两直线2x+my十1=0与mx+y-1=0平行的充分不必要条件，本选项为假命题；
②由圆的方程得到圆心坐标为（cosθ，sinθ），半径r=1，
得到此圆是圆心在原点的单位圆，而y=kx为过原点的直线，故直线与圆横有公共点，本选项为真命题；
③当x＞0且x≠1时，得到lgx＜0或lgx＞0，
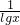当lgx＜0时，lgx+=-[（-lgx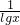）+（-）]≥-2，本命题为假命题；
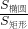④由题意可得：=P_{黄豆落在椭圆内}，
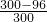即S_椭圆=×12=8.16，本命题为真命题．
综上，正确命题的序号为②④．
故答案为：②④
点评：此题考查学生掌握两直线平行时满足的条件，掌握直线与圆的位置关系的判别方法，理解利用基本不等式的条件，掌握利用模拟方法来估算概率，是一道中档题．