
【题目】已知函数![]() ,给出下列命题:①
,给出下列命题:①![]() 必是偶函数;②当
必是偶函数;②当![]() 时,
时,![]() 的图像关于直线
的图像关于直线![]() 对称;③若
对称;③若![]() ,则
,则![]() 在区间
在区间![]() 上是增函数;④若
上是增函数;④若![]() ,在区间
,在区间![]() 上
上![]() 有最大值
有最大值![]() . 其中正确的命题序号是:( )
. 其中正确的命题序号是:( )
A. ③ B. ②③ C. ③④ D. ①②③
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+φ)(x∈R)(其中A>0,ω>0,0<φ<![]() )的周期为π,且图象上一个最低点为M(
)的周期为π,且图象上一个最低点为M(![]() ,﹣2)
,﹣2)
(1)求f(x)的解析式
(2)求f(x)的单调增区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() 为偶函数,且当
为偶函数,且当![]() 时,
时,![]() .记
.记![]() .给出下列关于函数
.给出下列关于函数![]() 的说法:①当
的说法:①当![]() 时,
时,![]() ;②函数
;②函数![]() 为奇函数;③函数
为奇函数;③函数![]() 在
在![]() 上为增函数;④函数
上为增函数;④函数![]() 的最小值为
的最小值为![]() ,无最大值. 其中正确的是________.
,无最大值. 其中正确的是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆![]() 的左、右焦点为
的左、右焦点为![]() ,右顶点为
,右顶点为![]() ,上顶点为
,上顶点为![]() ,若
,若![]() ,
, ![]() 与
与![]() 轴垂直,且
轴垂直,且![]() .
.
(1)求椭圆方程;
(2)过点![]() 且不垂直于坐标轴的直线与椭圆交于
且不垂直于坐标轴的直线与椭圆交于![]() 两点,已知点
两点,已知点![]() ,当
,当![]() 时,求满足
时,求满足![]() 的直线
的直线![]() 的斜率
的斜率![]() 的取值范围.
的取值范围.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义区间![]() 的长度
的长度![]() 均为
均为![]() ,多个互无交集的区间的并集长度为各区间长度之和,例如
,多个互无交集的区间的并集长度为各区间长度之和,例如![]() 的长度
的长度![]() 。用
。用![]() 表示不超过
表示不超过![]() 的最大整数,例如
的最大整数,例如![]() 。记
。记![]() 。设
。设![]() ,
,![]() ,若用
,若用![]() 、
、![]() 和
和![]() 分别表示不等式
分别表示不等式![]() 、方程
、方程![]() 和不等式
和不等式![]() 解集区间的长度,则当
解集区间的长度,则当![]() 时,
时,![]() ____________.
____________.
查看答案和解析>>
科目:高中数学 来源: 题型:
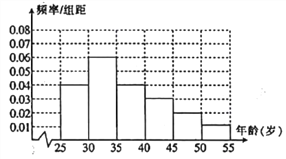
【题目】某高校进行社会实践,对![]() 岁的人群随机抽取 1000 人进行了一次是否开通“微博”的调查,开通“微博”的为“时尚族”,否则称为“非时尚族”.通过调查得到到各年龄段人数的频率分布直方图如图所示,其中在
岁的人群随机抽取 1000 人进行了一次是否开通“微博”的调查,开通“微博”的为“时尚族”,否则称为“非时尚族”.通过调查得到到各年龄段人数的频率分布直方图如图所示,其中在![]() 岁,
岁, ![]() 岁年龄段人数中,“时尚族”人数分别占本组人数的
岁年龄段人数中,“时尚族”人数分别占本组人数的![]() 、
、![]() .
.
(1)求![]() 岁与
岁与![]() 岁年龄段“时尚族”的人数;
岁年龄段“时尚族”的人数;
(2)从![]() 岁和
岁和![]() 岁年龄段的“时尚族”中,采用分层抽样法抽取6人参加网络时尚达人大赛,其中两人作为领队.求领队的两人年龄都在
岁年龄段的“时尚族”中,采用分层抽样法抽取6人参加网络时尚达人大赛,其中两人作为领队.求领队的两人年龄都在![]() 岁内的概率。
岁内的概率。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com