
如图,设 是棱长为
是棱长为 的正方体的一个顶点,过从顶点
的正方体的一个顶点,过从顶点 出发的三条棱的中点作截面,对正方体的所有顶点都如此操作,截去
出发的三条棱的中点作截面,对正方体的所有顶点都如此操作,截去 个三棱锥,所得的各截面与正方体各面共同围成一个多面体,则关于此多面体有以下结论:
个三棱锥,所得的各截面与正方体各面共同围成一个多面体,则关于此多面体有以下结论:
① 有 个顶点; ②
有
个顶点; ②
有 条棱; ③
有
条棱; ③
有 个面;
个面;
④ 表面积为 ; ⑤
体积为
; ⑤
体积为 .
.
其中正确的结论是 (写出所有正确结论的编号).

科目:高中数学 来源: 题型:
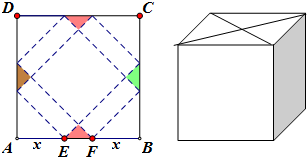 请你设计一个包装盒,如图所示,ABCD是边长为60cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得A,B,C,D四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,E、F在AB上,是被切去的等腰直角三角形斜边的两个端点,设AE=FB=x(cm).
请你设计一个包装盒,如图所示,ABCD是边长为60cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得A,B,C,D四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,E、F在AB上,是被切去的等腰直角三角形斜边的两个端点,设AE=FB=x(cm).查看答案和解析>>
科目:高中数学 来源: 题型:

查看答案和解析>>
科目:高中数学 来源: 题型:
(04年上海卷)(16分)
如图,P-ABC是底面边长为1的正三棱锥,D、E、F分别为棱长PA、PB、PC上的点, 截面DEF∥底面ABC, 且棱台DEF-ABC与棱锥P-ABC的棱长和相等.(棱长和是指多面体中所有棱的长度之和)
(1) 证明:P-ABC为正四面体;
(2) 若PD=![]() PA, 求二面角D-BC-A的大小;(结果用反三角函数值表示)
PA, 求二面角D-BC-A的大小;(结果用反三角函数值表示)
(3) 设棱台DEF-ABC的体积为V, 是否存在体积为V且各棱长均相等的直
平行六面体,使得它与棱台DEF-ABC有相同的棱长和? 若存在,请具体构造
出这样的一个直平行六面体,并给出证明;若不存在,请说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
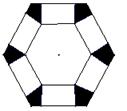
如图,把边长为![]() 的正六边形纸板剪去相同的六个角,做成一个底面为正六边形的无盖六棱柱盒子,设高为
的正六边形纸板剪去相同的六个角,做成一个底面为正六边形的无盖六棱柱盒子,设高为![]() ,所做成的盒子体积为
,所做成的盒子体积为![]() (不计接缝)。
(不计接缝)。
(1)写出体积![]() 与高
与高![]() 的函数关系式;(2)当
的函数关系式;(2)当![]() 为多少时,体积
为多少时,体积![]() 最大,最大值是多少?
最大,最大值是多少?
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江苏省泰州市泰兴三中高二(上)期中数学试卷(解析版) 题型:解答题
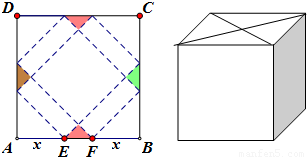 请你设计一个包装盒,如图所示,ABCD是边长为60cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得A,B,C,D四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,E、F在AB上,是被切去的等腰直角三角形斜边的两个端点,设AE=FB=x(cm).
请你设计一个包装盒,如图所示,ABCD是边长为60cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得A,B,C,D四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,E、F在AB上,是被切去的等腰直角三角形斜边的两个端点,设AE=FB=x(cm).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com