
��04���Ϻ�����(16��)
��ͼ,P-ABC�ǵ���߳�Ϊ1��������,D��E��F�ֱ�Ϊ�ⳤPA��PB��PC�ϵĵ�, ����DEF�ε���ABC, ����̨DEF-ABC����P-ABC���ⳤ�����.(�ⳤ����ָ��������������ij���֮��)
(1) ֤����P-ABCΪ�������壻
(2) ��PD=![]() PA, ������D-BC-A�Ĵ�С��(����÷����Ǻ���ֵ��ʾ)
PA, ������D-BC-A�Ĵ�С��(����÷����Ǻ���ֵ��ʾ)
(3) ����̨DEF-ABC�����ΪV, �Ƿ�������ΪV�Ҹ��ⳤ����ȵ�ֱ
ƽ��������,ʹ��������̨DEF-ABC����ͬ���ⳤ��? ������,����幹��
��������һ��ֱƽ��������,������֤������������,��˵������.

��������֤����(1) ����̨DEF-ABC����P-ABC���ⳤ�����,
��DE+EF+FD=PD+OE+PF.
�߽֡���DEF�ε���ABC,
��DE=EF=FD=PD=OE=PF,��DPE=��EPF=��FPD=60��, ��P-ABC����������.
���⡿(2)ȡBC���е�M,����PM,DM.AM.
��BC��PM,BC��AM, ��BC��ƽ��PAM,BC��DM,
���DMAΪ�����D-BC-A��ƽ���.
��(1)֪,P-ABC�ĸ��ⳤ��Ϊ1,
��PM=AM=![]() ,��D��PA���е�,��
,��D��PA���е�,��
sin��DMA=![]() ,���DMA=arcsin
,���DMA=arcsin![]() .
.
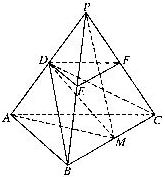
(3)��������������ֱƽ��������.
��̨DEF-ABC���ⳤ��Ϊ��ֵ6,���ΪV.
��ֱƽ����������ⳤ��Ϊ![]() ,�����������н�Ϊ��,
,�����������н�Ϊ��,
����������ⳤ��Ϊ6, ���Ϊ![]() sin��=V.
sin��=V.
����������P-ABC�������![]() ,��0<V<
,��0<V<![]() ,0<8V<1.��֪��=arcsim(8V)
,0<8V<1.��֪��=arcsim(8V)
�ʹ����ⳤ��Ϊ![]() ,�����������н�Ϊarcsim(8V)��ֱƽ�������弴����Ҫ��.
,�����������н�Ϊarcsim(8V)��ֱƽ�������弴����Ҫ��.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
��04���Ϻ�����(14��)
�Ǻ���f(x)=![]() �Ķ�����ΪA, g(x)=lg[(x��a��1)(2a��x)](a<1) �Ķ�����ΪB.
�Ķ�����ΪA, g(x)=lg[(x��a��1)(2a��x)](a<1) �Ķ�����ΪB.
(1) ��A��
(2) ��B![]() A, ��ʵ��a��ȡֵ��Χ.
A, ��ʵ��a��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��04���Ϻ�������(18��)
��P1(x1,y1), P1(x2,y2),��, Pn(xn,yn)(n��3,n��N) �Ƕ�������C�ϵĵ�, ��a1=![]() 2, a2=
2, a2=![]() 2, ��, an=
2, ��, an=![]() 2������һ������Ϊd(d��0) �ĵȲ�����, ����O������ԭ��. ��Sn=a1+a2+��+an.
2������һ������Ϊd(d��0) �ĵȲ�����, ����O������ԭ��. ��Sn=a1+a2+��+an.
(1) ��C�ķ���Ϊ![]() =1,n=3. ��P1(3,0) ��S3=255, ���P3�����ꣻ
=1,n=3. ��P1(3,0) ��S3=255, ���P3�����ꣻ
(ֻ��д��һ��)
(2)��C�ķ���Ϊ![]() (a>b>0). ��P1(a,0), ���ڸ�������Ȼ��n, ������d�仯ʱ, ��Sn����Сֵ��
(a>b>0). ��P1(a,0), ���ڸ�������Ȼ��n, ������d�仯ʱ, ��Sn����Сֵ��
. (3)��ѡ��һ������Բ��Ķ�������C��C�ϵ�һ��P1,���ڸ�������Ȼ��n,д�����������ĵ�P1, P2,��Pn���ڵij�Ҫ����,��˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
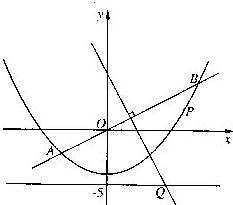
��04���Ϻ����ģ�(��������14��) ��1С������6��, ��2С������8��
��ͼ, ֱ��y=![]() x��������y=
x��������y=![]() x2��4����A��B����, �߶�AB�Ĵ�ֱƽ������ֱ��y=��5����Q��.
x2��4����A��B����, �߶�AB�Ĵ�ֱƽ������ֱ��y=��5����Q��.
(1) ���Q�����ꣻ
(2) ��PΪ��������λ���߶�AB�·�
(��A��B) �Ķ���ʱ, ��OPQ��������ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��04���Ϻ����ģ�(18��)
��P1(x1,y1), P1(x2,y2),��, Pn(xn,yn)(n��3,n��N) �Ƕ�������C�ϵĵ�, ��a1=![]() 2, a2=
2, a2=![]() 2, ��, an=
2, ��, an=![]() 2������һ������Ϊd(d��0) �ĵȲ�����, ����O������ԭ��. ��Sn=a1+a2+��+an.
2������һ������Ϊd(d��0) �ĵȲ�����, ����O������ԭ��. ��Sn=a1+a2+��+an.
(1) ��C�ķ���Ϊ![]() ��y2=1,n=3. ��P1(3,0) ��S3=162, ���P3�����ꣻ
��y2=1,n=3. ��P1(3,0) ��S3=162, ���P3�����ꣻ
(ֻ��д��һ��)
(2) ��C�ķ���Ϊy2=2px(p��0). ��P1(0,0), ���ڸ�������Ȼ��n, ֤����
(x1+p)2, (x2+p)2, ��,(xn+p)2�ɵȲ����У�
(3) ��C�ķ���Ϊ![]() (a>b>0). ��P1(a,0), ���ڸ�������Ȼ��n, ������d�仯ʱ, ��Sn����Сֵ.
(a>b>0). ��P1(a,0), ���ڸ�������Ȼ��n, ������d�仯ʱ, ��Sn����Сֵ.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com