
【题目】已知函数 ,
,![]() .
.
(1)若对任意实数![]() ,关于
,关于![]() 的方程:
的方程:![]() 总有实数解,求
总有实数解,求![]() 的取值范围;
的取值范围;
(2)若![]() ,求使关于
,求使关于![]() 的方程:
的方程:![]() 有三个实数解的
有三个实数解的![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)由题意得知函数![]() 的值域为
的值域为![]() ,根据二次函数的基本性质可得函数
,根据二次函数的基本性质可得函数![]() 在区间
在区间![]() 上的值域
上的值域![]() ,以及该函数在区间
,以及该函数在区间![]() 上的值域
上的值域![]() ,可得出
,可得出![]() ,从而可得出实数
,从而可得出实数![]() 的取值范围;
的取值范围;
(2)由题意得出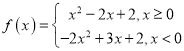 ,可知
,可知![]() 不是方程
不是方程![]() 的根,由参变量分离法得出
的根,由参变量分离法得出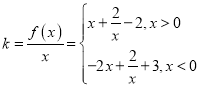 ,令
,令![]() ,将问题转化为直线
,将问题转化为直线![]() 与函数
与函数![]() 的图象有三个公共点,利用数形结合思想可得出实数
的图象有三个公共点,利用数形结合思想可得出实数![]() 的取值范围.
的取值范围.
(1)原问题等价为函数![]() 的值域为
的值域为![]() .
.
当![]() 时,
时,![]() ,
,
所以,函数![]() 在区间
在区间![]() 上的值域为
上的值域为![]() ;
;
当![]() 时,
时,![]() ,
,
则函数![]() 在区间
在区间![]() 上单调递增,此时
上单调递增,此时![]() .
.
所以,函数![]() 在区间
在区间![]() 上的值域为
上的值域为![]() .
.
由题意可得![]() ,
,![]() .
.
因此,实数![]() 的取值范围是
的取值范围是![]() ;
;
(2)当![]() 时,
时,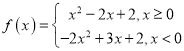 ,可知
,可知![]() 不是方程
不是方程![]() 的根,
的根,
当![]() 时,由
时,由![]() ,得
,得![]() ,令
,令![]() ,
,
则 ,所以,直线
,所以,直线![]() 与函数
与函数![]() 的图象有三个公共点.
的图象有三个公共点.
当![]() 时,由双勾函数的单调性可知,函数
时,由双勾函数的单调性可知,函数![]() 的单调递减区间为
的单调递减区间为![]() ,单调递增区间为
,单调递增区间为![]() ,此时,函数
,此时,函数![]() 取得最小值,即
取得最小值,即![]() ;
;
当![]() 时,
时,![]() ,
,
由于函数![]() 和函数
和函数![]() 都是减函数,则函数
都是减函数,则函数![]() 在区间
在区间![]() 上为减函数.
上为减函数.
作出函数![]() 和直线
和直线![]() 的图象如下图所示:
的图象如下图所示:
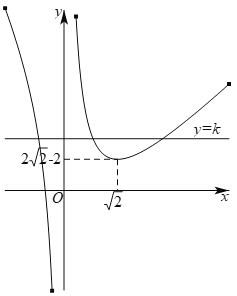
由图象可知,当![]() 时,直线
时,直线![]() 与函数
与函数![]() 的图象有三个交点,
的图象有三个交点,
因此,实数![]() 的取值范围是
的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】下列说法中,错误的是( )
A. 若命题![]() ,
,![]() ,则命题
,则命题![]() ,
,![]()
B. “![]() ”是“
”是“![]() ”的必要不充分条件
”的必要不充分条件
C. “若![]() ,则
,则![]() 、
、![]() 中至少有一个不小于
中至少有一个不小于![]() ”的逆否命题是真命题
”的逆否命题是真命题
D. ![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在国庆期间,某商场进行优惠大酬宾活动,在活动期间,商场内所有商品按标价的80%出售;同时,当顾客在该商场内消费满一定金额(![]() 元)后,还可按如下方案获得相应金额(
元)后,还可按如下方案获得相应金额(![]() 元)的奖券:
元)的奖券: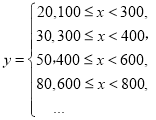 根据上述优惠方案,顾客在该商场购物可以获得双重优惠例如,购买标价为300元的商品,则消费金额为240元,获得的优惠额为:
根据上述优惠方案,顾客在该商场购物可以获得双重优惠例如,购买标价为300元的商品,则消费金额为240元,获得的优惠额为:![]() (元).设购买商品得到的
(元).设购买商品得到的![]() ,试问:
,试问:
(1)购买一件标价为800元的商品,顾客得到的优惠率是多少?
(2)对于标价在![]() (元)内的商品,要使顾客购买某商品获得30%的优惠率,则该商品的标价是多少?
(元)内的商品,要使顾客购买某商品获得30%的优惠率,则该商品的标价是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】第23届冬季奥运会于2018年2月9日至2月25日在韩国平昌举行,期间正值我市学校放寒假,寒假结束后,某校工会对全校教职工在冬季奥运会期间每天收看比赛转播的时间作了一次调查,得到如下频数分布表:

(1)若讲每天收看比赛转播时间不低于3小时的教职工定义为“体育达人”,否则定义为“非体育达人”,请根据频数分布表补全![]() 列联表:
列联表:

并判断能否有90%的把握认为该校教职工是否为“体育达人”与“性别”有关;
(2)在全校“体育达人”中按性别分层抽样抽取6名,再从这6名“体育达人”中选取2名作冬奥会知识讲座.记其中女职工的人数为![]() ,求的
,求的![]() 分布列与数学期望.
分布列与数学期望.
附表及公式:
![]()
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 、
、![]() 分别是椭圆
分别是椭圆![]() 的左、右焦点.若
的左、右焦点.若![]() 是该椭圆上的一个动点,
是该椭圆上的一个动点,![]() 的最大值为1.
的最大值为1.
(1)求椭圆![]() 的方程;
的方程;
(2)设直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,点
两点,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() (
(![]() 与
与![]() 不重合),则直线
不重合),则直线![]() 与
与![]() 轴是否交于一个定点?若是,请写出定点坐标,并证明你的结论;若不是,请说明理由.
轴是否交于一个定点?若是,请写出定点坐标,并证明你的结论;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,以坐标原点
,以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,直线
轴正半轴为极轴,建立极坐标系,直线![]() 的参数方程为
的参数方程为![]() (t为参数).
(t为参数).
(1)写出曲线![]() 的参数方程和直线
的参数方程和直线![]() 的普通方程;
的普通方程;
(2)已知点![]() 是曲线
是曲线![]() 上一点,,求点
上一点,,求点![]() 到直线
到直线![]() 的最小距离.
的最小距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中正确的个数①“![]() ,
,![]() ”的否定是“
”的否定是“![]() ,
,![]() ”;②用相关指数
”;②用相关指数![]() 可以刻画回归的拟合效果,
可以刻画回归的拟合效果,![]() 值越小说明模型的拟合效果越好;③命题“若
值越小说明模型的拟合效果越好;③命题“若![]() ,则
,则![]() ”的逆命题为真命题;④若
”的逆命题为真命题;④若![]()
![]() 的解集为
的解集为![]() ,则
,则![]() .
.
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com