
已知函数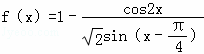 .
.
(Ⅰ)求函数f(x)的定义域;
(Ⅱ)求函数f(x)的单调增区间.
考点:
二倍角的余弦;正弦函数的定义域和值域;正弦函数的单调性.
专题:
三角函数的图像与性质.
分析:
(Ⅰ)由分母不为0,得到sin(x﹣![]() )≠0,利用正弦函数的性质即可求出函数f(x)的定义域;
)≠0,利用正弦函数的性质即可求出函数f(x)的定义域;
(Ⅱ)函数解析式第二项分子利用二倍角的余弦函数公式化简,第二项利用两角和与差的正弦函数公式化简,约分后再利用两角和与差的正弦函数公式化为一个角的正弦函数,根据正弦函数的单调性即可求出函数的单调递增区间.
解答:
解:(I)∵sin(x﹣![]() )≠0,
)≠0,
∴x﹣![]() ≠kπ,k∈Z,
≠kπ,k∈Z,
则函数的定义域为{x|x≠kπ+![]() ,k∈Z};
,k∈Z};
(II)∵f(x)=1﹣![]() =1+(cosx+sinx)=1+sinx+cosx=1+
=1+(cosx+sinx)=1+sinx+cosx=1+![]() sin(x+
sin(x+![]() ),
),
又∵y=sinx的单调递增区间为(2kπ﹣![]() ,2kπ+
,2kπ+![]() ),k∈Z,
),k∈Z,
令2kπ﹣![]() <x+
<x+![]() <2kπ+
<2kπ+![]() ,
,
解得:2kπ﹣![]() <x<2kπ+
<x<2kπ+![]() ,
,
又注意到x≠kπ+![]() ,
,
则f(x)的单调递增区间为(2kπ﹣![]() ,2kπ+
,2kπ+![]() ),k∈Z.
),k∈Z.
点评:
此题考查了二倍角的余弦函数公式,正弦函数的定义域和值域,以及正弦函数的单调性,熟练掌握公式是解本题的关键.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:高中数学 来源:2014届江西省高三上学期第二次月考文科数学试卷(解析版) 题型:解答题
已知函数
 .
.
(1)求函数 的单调递增区间;
的单调递增区间;
(2)若对任意 ,函数
,函数 在
在 上都有三个零点,求实数
上都有三个零点,求实数 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com