Question

12．在三棱锥P-ABC中，PA、PB、PC两两垂直，AC=BC=2PA=2PB=4，E、F分别是AC、BC的中点．
（1）判断直线AB与平面PEF的位置关系，并说明理由；
（2）求二面角E-PF-C的余弦值；
（3）在线段BC上是否存在一点Q，使AQ⊥PE？证明你的结论．

Answer 1

分析 （1）由E、F分别是AC、BC中点，得EF∥AB，即AB∥平面PEF．
（2）过M作MN⊥PF于点N，连结EN，则∠MNE是二面角E-PF-C的平面角．
在Rt△EMN中，EM=1，MN=$\frac{\sqrt{3}}{2}$，可得cos$∠MNE=\frac{\sqrt{21}}{7}$
即求得二面角E-DF-C的余弦值．
（3）在线段BC上存在点Q，使AQ⊥PE．
在线段BC上取点Q．使BQ=$\frac{1}{3}BC$，过Q作QR⊥PC于点R
则QR⊥平面PAC，可得PR=$\frac{1}{3}PC=\frac{2\sqrt{3}}{3}$，在Rt△PAR中，∠PAR=30°，即可得出结论．

解答 （1）解：如图：在△ABC中，由E、F分别是AC、BC中点，得EF∥AB（2分）
又AB?平面PEF，EF?平面PEF
∴AB∥平面PEF．（4分）
（2）解：∵AP⊥CP，AP⊥BP，CP、AP在平面PBC内
∴AP⊥平面PBC
取PC的中点M，连结EM，则EM∥PA
∴EM⊥平面PBC，故EM⊥PF
过M作MN⊥PF于点N，连结EN
则PF⊥平面EMN，∴则EN⊥PF
因此∠MNE是二面角E-PF-C的平面角．
在Rt△PBC中，∵PB=2，BC=4，∴PC=2$\sqrt{3}$，
∵F为BC中点，∴PB=PF=BF=2，∠FPC=30°
可得MN=PM×sin30°=$\frac{\sqrt{3}}{2}$
在Rt△EMN中，EM=1，MN=$\frac{\sqrt{3}}{2}$，∴EN=$\frac{\sqrt{7}}{2}$
故cos$∠MNE=\frac{\sqrt{21}}{7}$
即二面角E-DF-C的余弦值为$\frac{\sqrt{21}}{7}$（8分）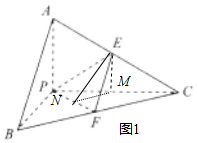



（3）解：在线段BC上存在点Q，使AQ⊥PE
证明如下：在线段BC上取点Q．使BQ=$\frac{1}{3}BC$，过Q作QR⊥PC于点R
则QR⊥平面PAC
∵PR=$\frac{1}{3}PC=\frac{2\sqrt{3}}{3}$，在Rt△PAR中，∠PAR=30°，
又PA=PE=AE=2，∴∠APE=60°
∴AR⊥PE
∴PE⊥平面AQR，因此AQ⊥PE（12分）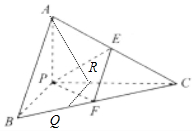

点评 本题考查了线面平行、线线平行的判定，考查了二面角的求法，属于中档题．