
对于下列命题:①在△ABC中,若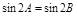 ,则△ABC为等腰三角形;②已知a, b,c是△ABC的三边长,若
,则△ABC为等腰三角形;②已知a, b,c是△ABC的三边长,若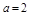 ,
,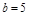 ,
,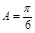 ,则△ABC有两组解;③设
,则△ABC有两组解;③设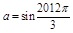 ,
,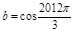 ,
,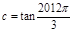 ,则
,则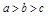 ;④将函数
;④将函数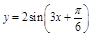 图象向左平移
图象向左平移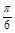 个单位,得到函数
个单位,得到函数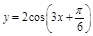 图象。其中正确命题的个数是 .
图象。其中正确命题的个数是 .
(3)(4)
解析试题分析:①,∵△ABC中,若sin2A=sin2B,∴2A=2B或2A+2B=π,∴△ABC为等腰三角形或直角三角形,故①错误;
②,∵a,b,c是△ABC的三边长,若a=2,b=5,A=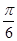 ,
,
∴由正弦定理得,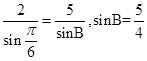 >1,这是不可能的,故②错误;
>1,这是不可能的,故②错误;
③,∵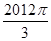 =335×2π+
=335×2π+ ,∴
,∴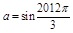 =sin
=sin =
=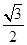 ,同理可得b=cos
,同理可得b=cos =-
=-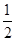 ,c=tan
,c=tan =-
=-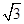 ,故a>b>c,③正确;
,故a>b>c,③正确;
④将函数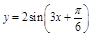 图象向左平移
图象向左平移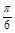 个单位,得:y=2sin[3(x+
个单位,得:y=2sin[3(x+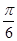 )+
)+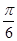 ]
]
=2sin[ +(3x+
+(3x+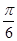 )]=
)]=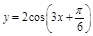 ,故④正确;
,故④正确;
故答案为(3)(4)。
考点:本题主要考查三角函数的图象和性质,正弦定理、余弦定理的应用。
点评:中档题,根据三角函数的性质与正弦定理对四个结论逐一进行判断,即可得到正确的结论。说明结论不成立,也可以通过选取特殊值,举反例。


科目:高中数学 来源: 题型:填空题
如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面店内两个观测点C与D,测得∠BCD=15°,∠BDC=30°,CD=30米,并在C测得塔顶A的仰角为60°,则塔的高度AB= 米。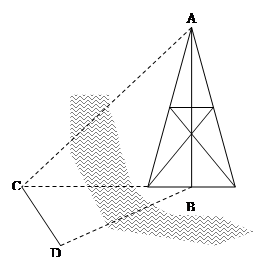
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
( 理科 )(1).(坐标系与参数方程选做题)已知在极坐标系下,点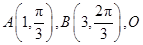 是极点,则
是极点,则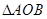 的面积等于_______;
的面积等于_______;
(2).(不等式选择题)关于 的不等式
的不等式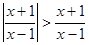 的解集是____ ____。
的解集是____ ____。
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
如图,甲船以每小时 海里的速度向正北方航行,乙船按固定方向匀速直线航行,当甲船位于
海里的速度向正北方航行,乙船按固定方向匀速直线航行,当甲船位于 处时,乙船位于甲船的北偏西
处时,乙船位于甲船的北偏西 方向的
方向的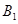 处,此时两船相距
处,此时两船相距 海里,当甲船航行
海里,当甲船航行 分钟到达
分钟到达 处时,乙船航行到甲船的北偏西
处时,乙船航行到甲船的北偏西 方向的
方向的 处,此时两船相距
处,此时两船相距 海里,则乙船每小时航行 海里?
海里,则乙船每小时航行 海里?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com