Question

若四面体各棱长是1或2，且该四面体不是正四面体，则其体积的值是________．(只须写出一个可能的值)

Answer 1

答案：
解析：

　　解析：该题的显著特点是结论发散而不惟一．本题表面上是考查锥体求积公式这个知识点，实际上主要考查由所给条件构造一个四面体的能力，首先得考虑每个面的三条棱是如何构成的．

　　排除{1，1，2}，可得{1，1，1}，{1，2，2}，{2，2，2}，然后由这三类面在空间构造满足条件的一个四面体，再求其体积．

　　由平时所见的题目，至少可构造出二类满足条件的四面体，五条边为2，另一边为1，对棱相等的四面体．

　　对于五条边为2，另一边为1的四面体，参看下图所示，设AD＝1，取AD的中点为M，平面BCM把三棱锥分成两个三棱锥，由对称性可知AD⊥面BCM，且V_A－BCM＝V_D－BCM，所以

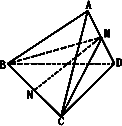
　　V_ABCD＝S_ΔBCM·AD．

　　CM＝＝＝．设N是BC的中点，则MN⊥BC，MN＝＝＝，从而S_ΔBCM＝×2×＝，

　　故V_ABCD＝××1＝．

　　对于对棱相等的四面体，可参见下图其体积的计算可先将其置于一个长方体之中，再用长方体的体积减去四个小三棱锥的体积来进行．亦可套公式V＝·，

　　不妨令a＝b＝2，c＝1，则

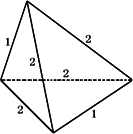
　　V＝·

　　＝·＝．