
已知函数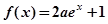 ,
,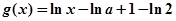 ,其中
,其中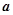 为常数,
为常数,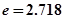 ,函数
,函数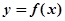 的图象与坐标轴交点处的切线为
的图象与坐标轴交点处的切线为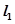 ,函数
,函数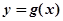 的图象与直线
的图象与直线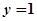 交点处的切线为
交点处的切线为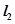 ,且
,且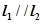 。
。
(Ⅰ)若对任意的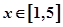 ,不等式
,不等式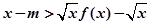 成立,求实数
成立,求实数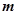 的取值范围.
的取值范围.
(Ⅱ)对于函数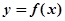 和
和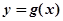 公共定义域内的任意实数
公共定义域内的任意实数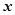 。我们把
。我们把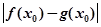 的值称为两函数在
的值称为两函数在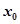 处的偏差。求证:函数
处的偏差。求证:函数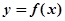 和
和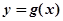 在其公共定义域的所有偏差都大于2.
在其公共定义域的所有偏差都大于2.
(Ⅰ)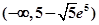 ;(Ⅱ)详见解析.
;(Ⅱ)详见解析.
解析试题分析:(Ⅰ)利用参数分离法将不等式问题转化为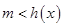 ,等价转化为
,等价转化为 处理,于是问题的核心就是求函数
处理,于是问题的核心就是求函数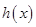 ,利用导数求解,但同时需要注意题中的隐含条件将
,利用导数求解,但同时需要注意题中的隐含条件将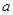 的值确定下来;(Ⅱ)先确定函数
的值确定下来;(Ⅱ)先确定函数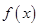 与函数
与函数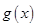 的解析式,然后引入函数
的解析式,然后引入函数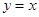 ,通过证明
,通过证明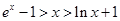 ,进而得到
,进而得到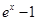
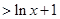 ,得到
,得到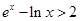 ,于是就说明原结论成立.
,于是就说明原结论成立.
试题解析:解(Ⅰ)函数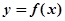 的图象与坐标轴的交点为
的图象与坐标轴的交点为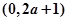 ,
,
又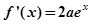

函数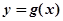 的图象与直线
的图象与直线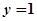 的交点为
的交点为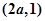 ,
,
又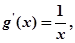
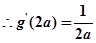
由题意可知, 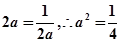
又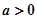 ,所以
,所以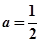 3分
3分
不等式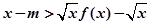 可化为
可化为
即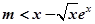
令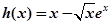 ,则
,则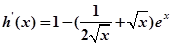 ,
,
又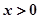 时,
时,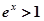 ,
,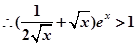 ,
,
故 ,
, 在
在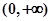 上是减函数
上是减函数
即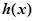 在
在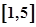 上是减函数
上是减函数
因此,在对任意的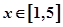 ,不等式
,不等式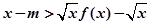 成立,
成立,
只需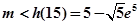
所以实数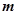 的取值范围是
的取值范围是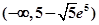 8分
8分
(Ⅱ)证明: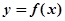 和
和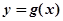 的公共定义域为
的公共定义域为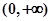 ,由(Ⅰ)可知
,由(Ⅰ)可知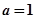 ,
,
令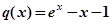 ,则
,则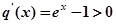 ,
,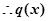 在
在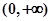 上是增函数
上是增函数
故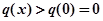 ,即
,即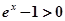 ①
①
令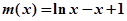 ,则
,则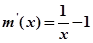 ,
,
当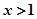 时,
时,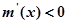 ;当
;当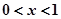 时,
时,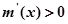 ,
,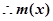 有最大值
有最大值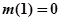 ,因此
,因此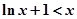 ②
②
由①②得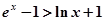 ,即
,即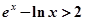
又由①得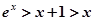
由②得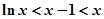
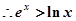
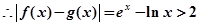
故函数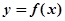 和
和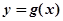 在其公共定义域的所有偏差都大于2
在其公共定义域的所有偏差都大于2


科目:高中数学 来源: 题型:解答题
已知函数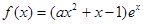 ,其中
,其中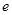 是自然对数的底数,
是自然对数的底数,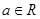 .
.
(1)若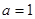 ,求曲线
,求曲线 在点
在点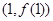 处的切线方程;
处的切线方程;
(2)若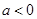 ,求
,求 的单调区间;
的单调区间;
(3)若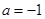 ,函数
,函数 的图象与函数
的图象与函数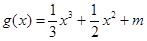 的图象有3个不同的交点,求实数
的图象有3个不同的交点,求实数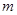 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某商场在店庆一周年开展“购物折上折活动”:商场内所有商品按标价的八折出售,折后价格每满500元再减100元.如某商品标价为1500元,则购买该商品的实际付款额为1500×0.8-200=1000(元).设购买某商品得到的实际折扣率 .设某商品标价为
.设某商品标价为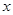 元,购买该商品得到的实际折扣率为
元,购买该商品得到的实际折扣率为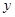 .
.
(Ⅰ)写出当 时,
时,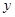 关于
关于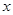 的函数解析式,并求出购买标价为1000元商品得到的实际折扣率;
的函数解析式,并求出购买标价为1000元商品得到的实际折扣率;
(Ⅱ)对于标价在[2500,3500]的商品,顾客购买标价为多少元的商品,可得到的实际折扣率低于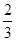 ?
?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数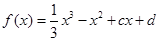
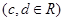 ,其图象为曲线
,其图象为曲线 ,点
,点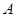 为曲线
为曲线 上的动点,在点
上的动点,在点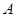 处作曲线
处作曲线 的切线
的切线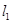 与曲线
与曲线 交于另一点
交于另一点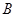 ,在点
,在点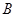 处作曲线
处作曲线 的切线
的切线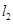 .
.
(Ⅰ)当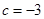 时,求函数
时,求函数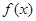 的单调区间;
的单调区间;
(Ⅱ)当点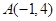 时,
时,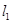 的方程为
的方程为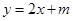 ,求实数
,求实数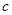 和
和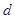 的值;
的值;
(Ⅲ)设切线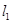 、
、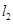 的斜率分别为
的斜率分别为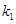 、
、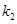 ,试问:是否存在常数
,试问:是否存在常数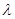 ,使得
,使得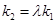 ?若存在,求出
?若存在,求出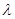 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(14分)已知函数 ,其中a是实数,设A(x1,f(x1)),B(x2,f(x2))为该函数图象上的点,且x1<x2.
,其中a是实数,设A(x1,f(x1)),B(x2,f(x2))为该函数图象上的点,且x1<x2.
(I)指出函数f(x)的单调区间;
(II)若函数f(x)的图象在点A,B处的切线互相垂直,且x2<0,求x2﹣x1的最小值;
(III)若函数f(x)的图象在点A,B处的切线重合,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某水域一艘装载浓硫酸的货船发生侧翻,导致浓硫酸泄漏,对河水造成了污染.为减少对环境的影响,环保部门迅速反应,及时向污染河道投入固体碱, 个单位的固体碱在水中逐渐溶化,水中的碱浓度
个单位的固体碱在水中逐渐溶化,水中的碱浓度 与时间
与时间 (小时)的关系可近似地表示为:
(小时)的关系可近似地表示为: ,只有当污染河道水中碱的浓度不低于
,只有当污染河道水中碱的浓度不低于 时,才能对污染产生有效的抑制作用.
时,才能对污染产生有效的抑制作用.
(Ⅰ) 如果只投放1个单位的固体碱,则能够维持有效的抑制作用的时间有多长?
(Ⅱ) 第一次投放1单位固体碱后,当污染河道水中的碱浓度减少到 时,马上再投放1个单位的固体碱,设第二次投放后水中碱浓度为
时,马上再投放1个单位的固体碱,设第二次投放后水中碱浓度为 ,求
,求 的函数式及水中碱浓度的最大值.(此时水中碱浓度为两次投放的浓度的累加)
的函数式及水中碱浓度的最大值.(此时水中碱浓度为两次投放的浓度的累加)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com