
已知函数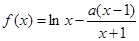 (
( ,
,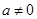 ),
), .
.
(1)求函数 的单调区间,并确定其零点个数;
的单调区间,并确定其零点个数;
(2)若 在其定义域内单调递增,求
在其定义域内单调递增,求 的取值范围;
的取值范围;
(3)证明不等式  (
( ).
).
(1)当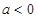 时,
时,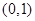 为
为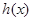 的减区间,
的减区间,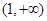 为
为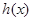 的增区间,
的增区间,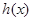 有且只有一个零点;当
有且只有一个零点;当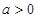 时,
时,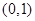 为
为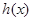 的增区间,
的增区间,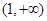 为
为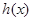 的减区间,
的减区间,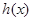 有且只有一个零点.
有且只有一个零点.
(2)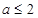
(3)由(2)可知 当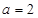 时,
时,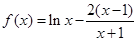 在
在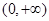 内单调递增,
内单调递增,
而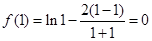 所以当
所以当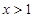 时,
时,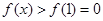 即
即 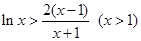 放缩法来得到。
放缩法来得到。
解析试题分析:解:(1)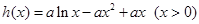 1分
1分
则 
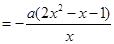
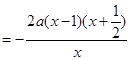 2分
2分
(i)若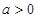 ,则当
,则当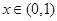 时,
时,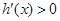 ;当
;当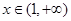 时,
时,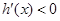
所以 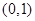 为
为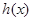 的增区间,
的增区间,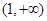 为
为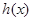 的减区间. 3分
的减区间. 3分
极大值为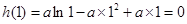
所以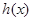 只有一个零点
只有一个零点 .
.
(ii)若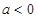 ,则当
,则当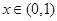 时,
时,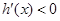 ;当
;当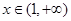 时,
时,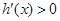
所以 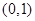 为
为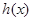 的减区间,
的减区间,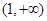 为
为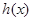 的增区间.
的增区间.
极小值为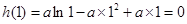 4分
4分
所以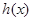 只有一个零点
只有一个零点 .
.
综上所述,
当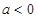 时,
时,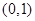 为
为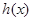 的减区间,
的减区间,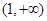 为
为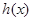 的增区间,
的增区间,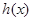 有且只有一个零点;
有且只有一个零点;
当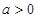 时,
时,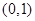 为
为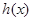 的增区间,
的增区间,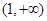 为
为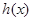 的减区间,
的减区间,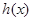 有且只有一个零点.
有且只有一个零点.
5分
(2) 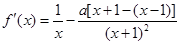

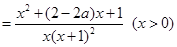 6分
6分
由 在其定义域内单调递增,可知
在其定义域内单调递增,可知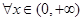 ,
,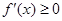 恒成立.
恒成立.
则 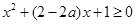
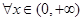 恒成立. 7分
恒成立. 7分
(法一)由二次函数的图象(开口向上,过定点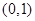 )可得
)可得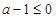 或
或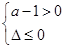
8分
则 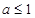 或
或
则 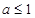 或
或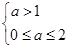
得 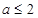 .
.
可以验证 当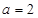 时
时 在其定义域
在其定义域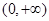 内单调递增
内单调递增
故 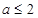 . 9分
. 9分
(法二)分离变量 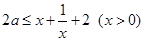
因 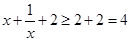 (当且仅当
(当且仅当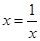 ,即
,即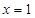 时取到等号) 8分
时取到等号) 8分
所以 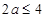 , 则
, 则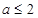 .
.
可以验证 当

 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:高中数学 来源: 题型:解答题
已知函数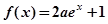 ,
,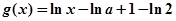 ,其中
,其中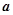 为常数,
为常数,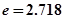 ,函数
,函数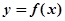 的图象与坐标轴交点处的切线为
的图象与坐标轴交点处的切线为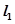 ,函数
,函数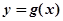 的图象与直线
的图象与直线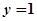 交点处的切线为
交点处的切线为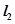 ,且
,且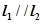 。
。
(Ⅰ)若对任意的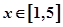 ,不等式
,不等式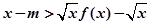 成立,求实数
成立,求实数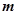 的取值范围.
的取值范围.
(Ⅱ)对于函数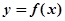 和
和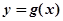 公共定义域内的任意实数
公共定义域内的任意实数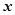 。我们把
。我们把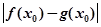 的值称为两函数在
的值称为两函数在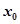 处的偏差。求证:函数
处的偏差。求证:函数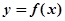 和
和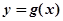 在其公共定义域的所有偏差都大于2.
在其公共定义域的所有偏差都大于2.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数 f(x)=ax+lnx,其中a为常数,设e为自然对数的底数.
(1)当a=-1时,求 的最大值;
的最大值;
(2)若f(x)在区间(0,e]上的最大值为-3,求a的值;
(3)当a=-1时,试推断方程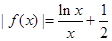 是否有实数解 .
是否有实数解 .
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知二次函数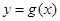 的导函数的图像与直线
的导函数的图像与直线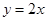 平行,且
平行,且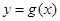 在
在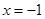 处取得极小值
处取得极小值 .设
.设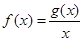 .
.
(1)若曲线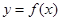 上的点
上的点 到点
到点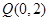 的距离的最小值为
的距离的最小值为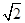 ,求
,求 的值;
的值;
(2) 如何取值时,函数
如何取值时,函数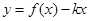 存在零点,并求出零点.
存在零点,并求出零点.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某工厂修建一个长方体无盖蓄水池,其容积为4 800立方米,深度为3米.池底每平方米的造价为150元,池壁每平方米的造价为120元.设池底长方形长为x米.
(1)求底面积,并用含x的表达式表示池壁面积;
(2)怎样设计水池能使总造价最低?最低造价是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,某动物园要建造两间完全相同的矩形熊猫居室,其总面积为24平方米,设熊猫居室的一面墙AD的长为x米 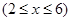 .
.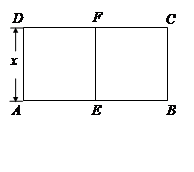
(1)用x表示墙AB的长;
(2)假设所建熊猫居室的墙壁造价(在墙壁高度一定的前提下)为每米1000元,请将墙壁的总造价y(元)表示为x(米)的函数;
(3)当x为何值时,墙壁的总造价最低?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com