
设函数 ,
,
 .
.
⑴ 求不等式 的解集;
的解集;
⑵ 如果关于 的不等式
的不等式 在
在 上恒成立,求实数
上恒成立,求实数 的取值范围.
的取值范围.
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:高中数学 来源: 题型:解答题
某工厂有 名工人,现接受了生产
名工人,现接受了生产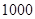 台
台 型高科技产品的总任务.已知每台
型高科技产品的总任务.已知每台 型产品由
型产品由 个
个 型装置和
型装置和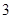 个
个 型装置配套组成,每个工人每小时能加工
型装置配套组成,每个工人每小时能加工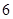 个
个 型装置或
型装置或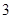 个
个 型装置.现将工人分成两组同时开始加工,每组分别加工一种装置(完成自己的任务后不再支援另一组).设加工
型装置.现将工人分成两组同时开始加工,每组分别加工一种装置(完成自己的任务后不再支援另一组).设加工 型装置的工人有
型装置的工人有 人,他们加工完
人,他们加工完 型装置所需时间为
型装置所需时间为 ,其余工人加工完
,其余工人加工完 型装置所需时间为
型装置所需时间为 (单位:小时,可不为整数).
(单位:小时,可不为整数).
(1)写出 、
、 的解析式;
的解析式;
(2)写出这 名工人完成总任务的时间
名工人完成总任务的时间 的解析式;
的解析式;
(3)应怎样分组,才能使完成总任务用的时间最少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某企业有两个生产车间,分别位于边长是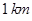 的等边三角形
的等边三角形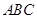 的顶点
的顶点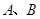 处(如图),现要在边
处(如图),现要在边 上的
上的 点建一仓库,某工人每天用叉车将生产原料从仓库运往车间,同时将成品运回仓库.已知叉车每天要往返
点建一仓库,某工人每天用叉车将生产原料从仓库运往车间,同时将成品运回仓库.已知叉车每天要往返 车间5次,往返
车间5次,往返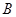 车间20次,设叉车每天往返的总路程为
车间20次,设叉车每天往返的总路程为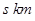 .(注:往返一次即先从仓库到车间再由车间返回仓库)
.(注:往返一次即先从仓库到车间再由车间返回仓库)
(Ⅰ)按下列要求确定函数关系式:
①设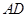 长为
长为 ,将
,将 表示成
表示成 的函数关系式;
的函数关系式;
②设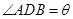 ,将
,将 表示成
表示成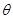 的函数关系式.
的函数关系式.
(Ⅱ)请你选用(Ⅰ)中一个合适的函数关系式,求总路程 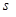 的最小值,并指出点
的最小值,并指出点 的位置.
的位置.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
渔场中鱼群的最大养殖量是m吨,为保证鱼群的生长空间,实际养殖量不能达到最大养殖量,必须留出适当的空闲量。已知鱼群的年增长量y吨和实际养殖量x吨与空闲率乘积成正比,比例系数为k(k>0).
写出y关于x的函数关系式,指出这个函数的定义域;
求鱼群年增长量的最大值;
当鱼群的年增长量达到最大值时,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数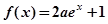 ,
,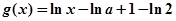 ,其中
,其中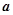 为常数,
为常数,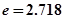 ,函数
,函数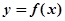 的图象与坐标轴交点处的切线为
的图象与坐标轴交点处的切线为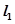 ,函数
,函数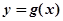 的图象与直线
的图象与直线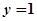 交点处的切线为
交点处的切线为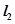 ,且
,且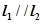 。
。
(Ⅰ)若对任意的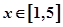 ,不等式
,不等式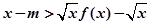 成立,求实数
成立,求实数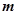 的取值范围.
的取值范围.
(Ⅱ)对于函数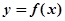 和
和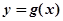 公共定义域内的任意实数
公共定义域内的任意实数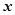 。我们把
。我们把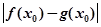 的值称为两函数在
的值称为两函数在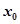 处的偏差。求证:函数
处的偏差。求证:函数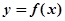 和
和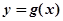 在其公共定义域的所有偏差都大于2.
在其公共定义域的所有偏差都大于2.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数 f(x)=ax+lnx,其中a为常数,设e为自然对数的底数.
(1)当a=-1时,求 的最大值;
的最大值;
(2)若f(x)在区间(0,e]上的最大值为-3,求a的值;
(3)当a=-1时,试推断方程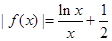 是否有实数解 .
是否有实数解 .
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某工厂修建一个长方体无盖蓄水池,其容积为4 800立方米,深度为3米.池底每平方米的造价为150元,池壁每平方米的造价为120元.设池底长方形长为x米.
(1)求底面积,并用含x的表达式表示池壁面积;
(2)怎样设计水池能使总造价最低?最低造价是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com