
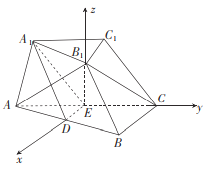
【题目】如图,在三棱台![]() 中,
中, ![]() ,
, ![]() 分别是
分别是![]() ,
, ![]() 的中点,
的中点, ![]() 平面
平面![]() ,
, ![]() 是等边三角形,
是等边三角形, ![]() ,
, ![]() ,
,![]() .
.

(1)证明: ![]() 平面
平面![]() ;
;
(2)求二面角![]() 的正弦值.
的正弦值.
【答案】(1)见解析;(2) ![]() .
.
【解析】试题分析:(1)根据棱台的性质和三角形的中位线可以得到![]() ,从而得到
,从而得到![]() 平面
平面![]() .在梯形
.在梯形![]() 中,
中, ![]() (
(![]() 为棱
为棱![]() 的中点),所以
的中点),所以![]() 平面
平面![]() ,从而可以证明平面
,从而可以证明平面![]() 平面
平面![]() ,也就能得到
,也就能得到![]() 平面
平面![]() .(2)以
.(2)以![]() 所在直线分别为
所在直线分别为![]() 轴,
轴, ![]() 轴,
轴, ![]() 轴,建立空间直角坐标系
轴,建立空间直角坐标系![]() ,通过计算平面
,通过计算平面![]() 和平面
和平面![]() 的法向量的夹角得到二面角
的法向量的夹角得到二面角![]() 的正弦值为
的正弦值为![]() .
.
解析:(1)证明:因为![]() ,
, ![]() 为棱
为棱![]() 的中点,所以
的中点,所以![]() ,所以四边形
,所以四边形![]() 为平行四边形,从而
为平行四边形,从而![]() .又
.又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() . 因为
. 因为![]() 是
是![]() 的中位线,所以
的中位线,所以![]() ,同理可证,
,同理可证, ![]() 平面
平面![]() .因为
.因为![]() ,所以平面
,所以平面![]() 平面
平面![]() . 又
. 又![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
(2)以![]() 所在直线分别为
所在直线分别为![]() 轴,
轴, ![]() 轴,
轴, ![]() 轴,建立如图所示的空间直角坐标系
轴,建立如图所示的空间直角坐标系![]() ,设
,设![]() ,则
,则![]() ,则
,则![]() .
.
设平面![]() 的一个法向量
的一个法向量![]() ,则
,则![]() 即
即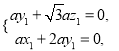
取![]() ,得
,得![]() .
.
同理,设平面![]() 的一个法向量
的一个法向量![]() ,又
,又![]() ,
,
由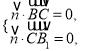 ,得
,得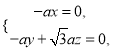 取
取![]() ,得
,得![]() .所以
.所以![]() ,即二面角
,即二面角![]() 的正弦值为
的正弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】据某市地产数据研究的数据显示,2016年该市新建住宅销售均价走势如下图所示,为抑制房价过快上涨,政府从8月采取宏观调控措施,10月份开始房价得到很好的抑制.
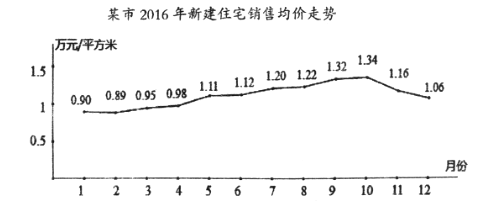
(1)地产数据研究院发现,3月至7月的各月均价![]() (万元/平方米)与月份
(万元/平方米)与月份![]() 之间具有较强的线性相关关系,试建立
之间具有较强的线性相关关系,试建立![]() 关于
关于![]() 的回归方程(系数精确到0.01);政府若不调控,依此相关关系预测第12月份该市新建住宅销售均价;
的回归方程(系数精确到0.01);政府若不调控,依此相关关系预测第12月份该市新建住宅销售均价;
(2)地产数据研究院在2016年的12个月份中,随机抽取三个月的数据作样本分析,若关注所抽三个月份的所属季度,记不同季度的个数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
参考数据: ![]() ,
, ![]() ,
, ![]() ;
;
回归方程![]() 中斜率和截距的最小二乘法估计公式分别为:
中斜率和截距的最小二乘法估计公式分别为:
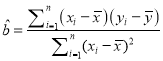 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
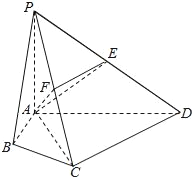
【题目】(14分)在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,PA=2AB=2.
(Ⅰ)求四棱锥P-ABCD的体积V;
(Ⅱ)若F为PC的中点,求证PC⊥平面AEF;
(Ⅲ)求证CE∥平面PAB.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为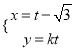 (
(![]() 为参数),直线
为参数),直线![]() 的参数方程为
的参数方程为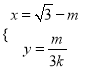 (
(![]() 为参数),设
为参数),设![]() 与
与![]() 的交点为
的交点为![]() ,当
,当![]() 变化时,
变化时, ![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)写出![]() 的普遍方程及参数方程;
的普遍方程及参数方程;
(2)以坐标原点为极点, ![]() 轴正半轴为极轴建立极坐标系,设曲线
轴正半轴为极轴建立极坐标系,设曲线![]() 的极坐标方程为
的极坐标方程为![]() ,
, ![]() 为曲线
为曲线![]() 上的动点,求点
上的动点,求点![]() 到
到![]() 的距离的最小值.
的距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,AB//CD,且![]()

(1)证明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC, ![]() ,且四棱锥P-ABCD的体积为
,且四棱锥P-ABCD的体积为![]() ,求该四棱锥的侧面积.
,求该四棱锥的侧面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com