练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    设函数。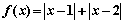

    （I）画出函数y=f(x)的图像；

    （II）若不等式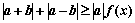，（a0,a、bR）恒成立，求实数x的范围.


    解：(I)----2分

     


                                

     (II)由|a+b|+|a-b|≥|a|f(x)

      恒成立   只需 

          ------7分


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


     

    （1）求函数f(x)的最大值及取得最大值时相应的x的值；

    （2）若函数y=f(2x)-a在区间上恰有两个零点，求tan()的值

    查看答案和解析>>

    科目：高中数学 来源： 题型：


     已知集合A＝{x|－x2＋3x＋10≥0}，B＝{x|m＋1≤x≤2m－1}，若BA，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知双曲线的两个焦点，点P是双曲线上一点，成等比数列，则双曲线的离心率为（  ）

         A 2     B 3      C    D 

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图，在三棱锥中，，，，．

    （Ⅰ）求证：；

    （Ⅱ）求二面角的的余弦值 .

     


    查看答案和解析>>

    科目：高中数学 来源： 题型：


    函数在处取到极值，则的值为(     )

        A.           B.          C.0             D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    棱长为2的正四面体在空间直角坐标系中移动，但保持点、分别在x轴、y轴上移动，则棱的中点到坐标原点O的最远距离为               （    ）

    A．             B．             C．            D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若a>b>1，P＝，Q＝(lg a＋lg b)，R＝lg()，则P、Q、R的大小关系为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    现有一个关于平面图形的命题：如图，同一个平面内有两个边长都是a的正方形，其中一个的某顶点在另一个的中心，则这两个正方形重叠部分的面积恒为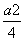.类比到空间，有两个棱长均为a的正方体，其中一个的某顶点在另一个的中心，则这两个正方体重叠部分的体积恒为________．

    查看答案和解析>>

    同步练习册答案