
 ,且样本容量160,则中间一组的频数为
,且样本容量160,则中间一组的频数为| A.32 | B.0.2 | C.40 | D.0.25 |
科目:高中数学 来源:不详 题型:填空题
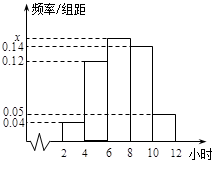
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 中随机抽取一个数,如果抽到的是7,则从
中随机抽取一个数,如果抽到的是7,则从 中应取的数是
中应取的数是 查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
A.通过最小二乘法得到的线性回归直线经过样本的中心 |
B.用最小二乘法求回归直线方程,是寻求使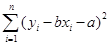 最小的a,b的值 最小的a,b的值 |
| C.相关系数r越小,表明两个变量相关性越弱 |
D. 越接近1,表明回归的效果越好 越接近1,表明回归的效果越好 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

 的值;
的值;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 (cm),相关行业质检部门规定:若
(cm),相关行业质检部门规定:若 ,则该零件为优等品;若
,则该零件为优等品;若 ,则该零件为中等品;其余零件为次品.现分别从甲、乙机床生产的零件中各随机抽取50件,经质量检测得到下表数据:
,则该零件为中等品;其余零件为次品.现分别从甲、乙机床生产的零件中各随机抽取50件,经质量检测得到下表数据:| 尺寸 | 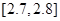 |  | 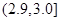 |  |  |  |
| 甲机床零件频数 | 2 | 3 | 20 | 20 | 4 | 1 |
| 乙机床零件频数 | 3 | 5 | 17 | 13 | 8 | 4 |
 .
.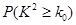 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com