
【题目】已知函数![]() .
.
(Ⅰ)求函数![]() 的最小值;
的最小值;
(Ⅱ)设![]() (
(![]() ),讨论函数
),讨论函数![]() 的单调性;
的单调性;
(Ⅲ)若斜率为![]() 的直线与曲线
的直线与曲线![]() 交于
交于![]() ,
,![]() 两点,其中
两点,其中![]() ,求证:
,求证:![]() .
.
【答案】(Ⅰ)![]() ;(Ⅱ)当
;(Ⅱ)当![]() 时,
时,![]() 在区间
在区间![]() 内是增函数,当
内是增函数,当![]() 时,
时,![]() 在
在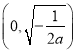 内单调递增,在
内单调递增,在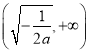 内单调递减.(Ⅲ)见解析.
内单调递减.(Ⅲ)见解析.
【解析】
试题分析:(Ⅰ)求函数![]() 的导数
的导数![]() ,由
,由![]() 与
与![]() 求函数的单调区间与单调性,从而可得
求函数的单调区间与单调性,从而可得![]() ;(Ⅱ)由已知可知
;(Ⅱ)由已知可知![]() ,
,![]() ,分
,分![]() 与
与![]() 分别讨论导数的符号可得函数
分别讨论导数的符号可得函数![]() 的单调区间;(Ⅲ)
的单调区间;(Ⅲ)![]() ,则不等式
,则不等式![]()
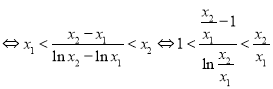 ,令
,令![]() ,只要证不等式
,只要证不等式![]() (
(![]() )即可,分别构造函数
)即可,分别构造函数![]() (
(![]() )与
)与![]() (
(![]() ),可证
),可证![]() 成立.
成立.
试题解析: (Ⅰ)![]() (
(![]() ),……(1分)
),……(1分)
令![]() ,得
,得![]() ,
,
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
则![]() 在
在![]() 内递减,在
内递减,在![]() 内递增,…………(2分)
内递增,…………(2分)
所以当![]() 时,函数
时,函数![]() 取得最小值,且
取得最小值,且![]() ……(3分)
……(3分)
(Ⅱ)![]() ,
,![]() (
(![]() ),…………(4分)
),…………(4分)
当![]() 时,恒有
时,恒有![]() ,
,![]() 在区间
在区间![]() 内是增函数;……(5分)
内是增函数;……(5分)
当![]() 时,令
时,令![]() ,即
,即![]() ,解得
,解得![]() ,
,
令![]() ,即
,即![]() ,解得
,解得![]() ,………(6分)
,………(6分)
综上,当![]() 时,
时,![]() 在区间
在区间![]() 内是增函数,当
内是增函数,当![]() 时,
时,![]() 在
在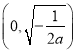 内单调递增,在
内单调递增,在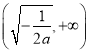 内单调递减.………(7分)
内单调递减.………(7分)
(Ⅲ)证明:![]() ,要证明
,要证明![]() ,
,
即证![]() ,………(8分)
,………(8分)
等价于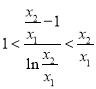 ,令
,令![]() (由
(由![]() ,知
,知![]() ),
),
则只需证![]() ,由
,由![]() ,知
,知![]() ,故等价于
,故等价于![]() (
(![]() )(
)(![]() )……(9分)
)……(9分)
①设![]() (
(![]() ),则
),则![]() (
(![]() ),所以
),所以![]() 在
在![]() 内是增函数,当
内是增函数,当![]() 时,
时,![]() ,所以
,所以![]() ;…………(10分)
;…………(10分)
②设![]() (
(![]() ),则
),则![]() (
(![]() ),所以
),所以![]() 在
在![]() 内是增函数,所以当
内是增函数,所以当![]() 时,
时,![]() ,即
,即![]() (
(![]() ).……(11分)
).……(11分)
由①②知(![]() )成立,所以
)成立,所以![]() .……(12分)
.……(12分)


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:高中数学 来源: 题型:
【题目】我们知道:人们对声音有不同的感觉,这与它的强度有关系.声音的强度![]() 用瓦/米2 (
用瓦/米2 (![]() )表示,但在实际测量时,常用声音的强度水平
)表示,但在实际测量时,常用声音的强度水平![]() 表示,它们满足以下公式:
表示,它们满足以下公式: ![]() (单位为分贝,
(单位为分贝, ![]() ,其中
,其中![]() ,这是人们平均能听到的最小强度,是听觉的开端).回答以下问题:
,这是人们平均能听到的最小强度,是听觉的开端).回答以下问题:
(1)树叶沙沙声的强度是![]() ,耳语的强度是
,耳语的强度是![]() ,恬静的无线电广播的强度是
,恬静的无线电广播的强度是![]() ,试分别求出它们的强度水平;
,试分别求出它们的强度水平;
(2)某一新建的安静小区规定:小区内公共场所的声音的强度水平必须保持在50分贝以下,试求声音强度![]() 的范围为多少?
的范围为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3+ax2+bx+a2.
(I)若f(x)在x=1处有极值10,求a,b的值;
(II)若当a=-1时,f(x)<0在x∈[1,2]恒成立,求b的取值范围
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)的最小值为1,且f(0)=f(2)=3.
(1)求f(x)的解析式;
(2)若f(x)在区间[2a,a+1]上不单调,求实数a的取值范围;
(3)在区间[-1,1]上,y=f(x)的图象恒在y=2x+2m+1的图象上方,试确定实数m的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋中装有偶数个球,其中红球、黑球各占一半,甲、乙、丙是三个空盒.每次从袋中任取两个球,将其中一个球放入甲盒,如果这个球是红球,就将另一个球放入乙盒,否则就放入丙盒.重复上述过程,直到袋中所有球都放入盒中,则( )
A. 乙盒中红球与丙盒中黑球一样多
B. 乙盒中黑球不多于丙盒中黑球
C. 乙盒中红球不多于丙盒中红球
D. 乙盒中黑球与丙盒中红球一样多
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2015年12月,京津冀等地数城市指数“爆表”,北方此轮污染为2015年以来最严重的污染过程,为了探究车流量与![]() 的浓度是否相关,现采集到北方某城市2015年12月份某星期星期一到星期日某一时间段车流量与
的浓度是否相关,现采集到北方某城市2015年12月份某星期星期一到星期日某一时间段车流量与![]() 的数据如表:
的数据如表:
时间 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 | 星期七 |
车流量 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 28 | 30 | 35 | 41 | 49 | 56 | 62 |
(1)由散点图知![]() 与
与![]() 具有线性相关关系,求
具有线性相关关系,求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)(i)利用(1)所求的回归方程,预测该市车流量为8万辆时![]() 的浓度;
的浓度;
(ii)规定:当一天内![]() 的浓度平均值在
的浓度平均值在![]() 内,空气质量等级为优;当一天内
内,空气质量等级为优;当一天内![]() 的浓度平均值在
的浓度平均值在![]() 内,空气质量等级为良,为使该市某日空气质量为优或者为良,则应控制当天车流量在多少万辆以内?(结果以万辆为单位,保留整数)
内,空气质量等级为良,为使该市某日空气质量为优或者为良,则应控制当天车流量在多少万辆以内?(结果以万辆为单位,保留整数)
参考公式:回归直线的方程是![]() ,其中
,其中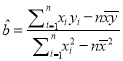 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,以原点
中,以原点![]() 为极点,以
为极点,以![]() 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的直角坐标方程并指出其形状;
的直角坐标方程并指出其形状;
(2)设![]() 是曲线
是曲线![]() 上的动点,求
上的动点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
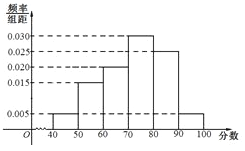
【题目】上周某校高三年级学生参加了数学测试,年部组织任课教师对这次考试进行成绩分析.现从中抽取80名学生的数学成绩(均为整数)的频率分布直方图如图所示.
(Ⅰ)估计这次月考数学成绩的平均分和众数;
(Ⅱ)假设抽出学生的数学成绩在![]() 段各不相同,且都超过94分.若将频率视为概率,现用简单随机抽样的方法,从95,96,97,98,99,100这6个数字中任意抽取2个数,有放回地抽取3次,记这3次抽取中恰好有两名学生的数学成绩的次数为
段各不相同,且都超过94分.若将频率视为概率,现用简单随机抽样的方法,从95,96,97,98,99,100这6个数字中任意抽取2个数,有放回地抽取3次,记这3次抽取中恰好有两名学生的数学成绩的次数为![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com