
分析 求椭圆的离心率,即求参数a,c的关系,本题中给出了三角形PF1F2为等腰直角三角形这一条件,由相关图形知,角P或角F1或角F2为直角,不妨令角P或角F2为直角,则有OP=OF1,或PF2=F1F2,求出两线段的长度,运用a,b,c的关系和离心率公式,整理即可得到所求的离心率.
解答 解:由△PF1F2是等腰直角三角形,
若P为直角顶点,即有OP=OF1,
即为b=c,即有a=$\sqrt{{b}^{2}+{c}^{2}}$=$\sqrt{2}$c,
则e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$;
若角F1或角F2为直角,不妨令角F2为直角,
此时P(c,y),
代入椭圆方程$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1,
解得y=±$\frac{{b}^{2}}{a}$,
又三角形PF1F2为等腰直角三角形,得PF2=F1F2,
故得$\frac{{b}^{2}}{a}$=2c,即2ac=a2-c2,
即e2+2e-1=0,解得e=-1±$\sqrt{2}$,
由0<e<1可得e=$\sqrt{2}$-1.
故椭圆的离心率是$\frac{\sqrt{2}}{2}$或$\sqrt{2}$-1.
故答案为:$\frac{\sqrt{2}}{2}$或$\sqrt{2}$-1.
点评 本题考查椭圆的方程、性质和应用,解题时要注意分类讨论的思想方法和公式的合理运用.


科目:高中数学 来源: 题型:解答题
 已知函数g(x)=Asin(ωx+φ)(其中A>0,|φ|<$\frac{π}{2}$,ω>0)的图象如图所示,函数f(x)=g(x)+$\frac{\sqrt{3}}{2}$cos2x-$\frac{3}{2}$sin2x
已知函数g(x)=Asin(ωx+φ)(其中A>0,|φ|<$\frac{π}{2}$,ω>0)的图象如图所示,函数f(x)=g(x)+$\frac{\sqrt{3}}{2}$cos2x-$\frac{3}{2}$sin2x查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 方程①有实根或方程②无实根 | B. | 方程①有实根或方程②有实根 | ||
| C. | 方程①无实根或方程②无实根 | D. | 方程①无实根或方程②有实根 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
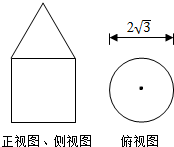 如图,一个简单组合体的正视图和侧视图都是由一个正方形与一个正三角形构成的相同的图形,俯视图是一个半径为$\sqrt{3}$的圆(包括圆心).则该组合体的表面积(各个面的面积的和)等于21π.
如图,一个简单组合体的正视图和侧视图都是由一个正方形与一个正三角形构成的相同的图形,俯视图是一个半径为$\sqrt{3}$的圆(包括圆心).则该组合体的表面积(各个面的面积的和)等于21π.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com