
| cosA |
| cosB |
| b |
| a |
| 4 |
| 3 |
| π |
| 2 |
| cosA |
| cosB |
| sinB |
| sinA |
| π |
| 2 |
| b |
| a |
| 4 |
| 3 |
| π |
| 2 |
| π |
| 2 |

| 3 |
| sinθ |
| 4 |
| cosθ |
| 12 |
| sinθcosθ |
| 24 |
| sin2θ |


科目:高中数学 来源: 题型:
 如图(1),在三角形ABC中,AB⊥AC,若AD⊥BC,则AB2=BD.BC;若类比该命题,如图(2),三棱锥A-BCD中,AD⊥面ABC,若A点在三角形BCD所在平面内的射影为M,则有什么结论?命题是否是真命题.
如图(1),在三角形ABC中,AB⊥AC,若AD⊥BC,则AB2=BD.BC;若类比该命题,如图(2),三棱锥A-BCD中,AD⊥面ABC,若A点在三角形BCD所在平面内的射影为M,则有什么结论?命题是否是真命题.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在三棱锥S-ABC中,侧面SAB⊥底面ABC,且∠ASB=∠ABC=90°,AS=SB=2,AC=2
如图,在三棱锥S-ABC中,侧面SAB⊥底面ABC,且∠ASB=∠ABC=90°,AS=SB=2,AC=2| 3 |
| 2S |
| l |
 C.
C.| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2S |
| l |
查看答案和解析>>
科目:高中数学 来源:海南省嘉积中学2009-2010学年高二上学期期末考试数学试卷(文) 题型:044
如图(1),在三角形ABC中,AB⊥AC,若AD⊥BC,则AB2=BD·BC;若类比该命题,如图(2),三棱锥A-BCD中,AD⊥面ABC,若A点在三角形BCD所在平面内的射影为M,则有什么结论?并给予证明.
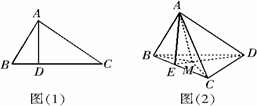
查看答案和解析>>
科目:高中数学 来源:2012-2013学年吉林省吉林一中高二(下)期末数学试卷(文科)(解析版) 题型:解答题
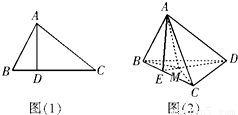 如图(1),在三角形ABC中,AB⊥AC,若AD⊥BC,则AB2=BD.BC;若类比该命题,如图(2),三棱锥A-BCD中,AD⊥面ABC,若A点在三角形BCD所在平面内的射影为M,则有什么结论?命题是否是真命题.
如图(1),在三角形ABC中,AB⊥AC,若AD⊥BC,则AB2=BD.BC;若类比该命题,如图(2),三棱锥A-BCD中,AD⊥面ABC,若A点在三角形BCD所在平面内的射影为M,则有什么结论?命题是否是真命题.查看答案和解析>>
科目:高中数学 来源:《第2章 推理与证明》2010年单元测试卷(解析版) 题型:解答题
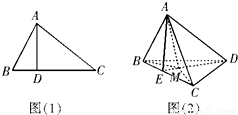 如图(1),在三角形ABC中,AB⊥AC,若AD⊥BC,则AB2=BD.BC;若类比该命题,如图(2),三棱锥A-BCD中,AD⊥面ABC,若A点在三角形BCD所在平面内的射影为M,则有什么结论?命题是否是真命题.
如图(1),在三角形ABC中,AB⊥AC,若AD⊥BC,则AB2=BD.BC;若类比该命题,如图(2),三棱锥A-BCD中,AD⊥面ABC,若A点在三角形BCD所在平面内的射影为M,则有什么结论?命题是否是真命题.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com