
 某校收集该校学生从家到学校的时间后,制作成如下的频率分布直方图:
某校收集该校学生从家到学校的时间后,制作成如下的频率分布直方图:分析 (1)根据频率和为1,列方程求出a的值,再计算平均到校时间;
(2)原问题等价于求到校时间的中位数,列式计算即可.
解答 解:(1)根据频率和为1,列出方程
(0.009+0.020+0.011+a+0.003+0.002)×20=1,
解得a=0.005;
计算平均到校时间为
$\overline x=({10×0.009+30×0.020+50×0.011+70×0.005+90×0.003+110×0.002})×20=41.6$(分钟)
(2)原问题等价于求到校时间的中位数,
列式计算:${x_0}=40-\frac{0.009×20+0.020×20-0.5}{0.020×20}×20=36$(分钟),
所以,从家到校时间36分钟以上开始住校.
点评 本题考查了频率分布直方图与求平均数、中位数的应用问题,是基础题目.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | 都大于4 | B. | 都小于4 | ||
| C. | 至少有一个大于4 | D. | 至少有一个不小于4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{100}+\frac{y^2}{96}=1$ | B. | $\frac{x^2}{25}+\frac{y^2}{21}=1$ | C. | $\frac{x^2}{96}+\frac{y^2}{100}=1$ | D. | $\frac{x^2}{21}+\frac{y^2}{25}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若a∥b,a∥α,则b∥α | B. | 若a⊥b,a⊥α,则b⊥α | ||
| C. | 若a∥α,a∥β,α∩β=b,则a∥b | D. | 若a∥α,α⊥β,则a⊥β |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
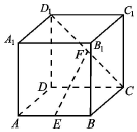 正方体ABCD-A1B1C1D1中,E为AB中点,F为CD1中点.
正方体ABCD-A1B1C1D1中,E为AB中点,F为CD1中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com