
已知函数f(x)=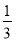 ax3-
ax3-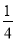 x2+cx+d(a,c,d∈R)满足f(0)=0,f′(1)=0,且f′(x)≥0在R上恒成立.
x2+cx+d(a,c,d∈R)满足f(0)=0,f′(1)=0,且f′(x)≥0在R上恒成立.
(1)求a,c,d的值;
(2)若h(x)=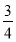 x2-bx+
x2-bx+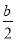 -
-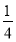 ,解不等式f′(x)+h(x)<0.
,解不等式f′(x)+h(x)<0.
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷2练习卷(解析版) 题型:选择题
已知向量a,b满足|a|=2,|b|=1,且(a+b)⊥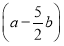 ,则a与b的夹角为( ).
,则a与b的夹角为( ).
A.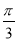 B.
B.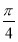 C.
C.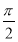 D.
D.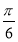
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练4练习卷(解析版) 题型:解答题
(2013·重庆卷)设f(x)=a(x-5)2+6ln x,其中a∈R,曲线y=f(x)在点(1,f(1))处的切线与y轴相交于点(0,6).
(1)确定a的值;
(2)求函数f(x)的单调区间与极值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练4练习卷(解析版) 题型:选择题
已知函数f(x)=x3+ax2+x+2(a>0)的极大值点和极小值点都在区间(-1,1)内,则实数a的取值范围是( ).
A.(0,2] B.(0,2) C.[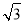 ,2) D.(
,2) D.(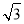 ,2)
,2)
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练3练习卷(解析版) 题型:选择题
已知a>0,x,y满足约束条件 若z=2x+y的最小值为1,则a等于( ).,
若z=2x+y的最小值为1,则a等于( ).,

A.  B.
B. C.1 D.2
C.1 D.2
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练2练习卷(解析版) 题型:解答题
设函数f(x)=ax2+bx+b-1(a≠0).
(1)当a=1,b=-2时,求函数f(x)的零点;
(2)若对任意b∈R,函数f(x)恒有两个不同零点,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练1练习卷(解析版) 题型:选择题
函数f(x)=log2|x|,g(x)=-x2+2,则f(x)·g(x)的图象只可能是( ).

查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习5-2空间向量与立体几何练习卷(解析版) 题型:选择题
长方体ABCD-A1B1C1D1中,AB=AA1=2,AD=1,E为CC1的中点,则异面直线BC1与AE所成角的余弦值为( ).
A. 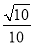 B.
B. 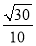 C.
C. 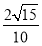 D.
D. 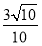
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com