
(2013·重庆卷)设f(x)=a(x-5)2+6ln x,其中a∈R,曲线y=f(x)在点(1,f(1))处的切线与y轴相交于点(0,6).
(1)确定a的值;
(2)求函数f(x)的单调区间与极值.
(1)a=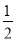 (2)极小值2+6ln 3. 极大值f(2)=
(2)极小值2+6ln 3. 极大值f(2)=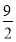 +6ln 2,f(x)在(0,2),(3,+∞)上为增函数;
+6ln 2,f(x)在(0,2),(3,+∞)上为增函数;
当2<x<3时,f′(x)<0,故f(x)在(2,3)上为减函数.
【解析】(1)因f(x)=a(x-5)2+6ln x,
故f′(x)=2a(x-5)+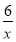 .
.
令x=1,得f(1)=16a,f′(1)=6-8a,
所以曲线y=f(x)在点(1,f(1))处的切线方程为
y-16a=(6-8a)(x-1),
由点(0,6)在切线上可得6-16a=8a-6,故a=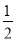 .
.
(2)由(1)知,f(x)=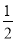 (x-5)2+6ln x(x>0),
(x-5)2+6ln x(x>0),
f′(x)=x-5+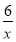 =
=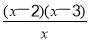 .
.
令f′(x)=0,解得x=2或3.
当0<x<2或x>3时,f′(x)>0,
故f(x)在(0,2),(3,+∞)上为增函数;
当2<x<3时,f′(x)<0,故f(x)在(2,3)上为减函数.
由此可知f(x)在x=2处取得极大值f(2)=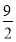 +6ln 2,在x=3处取得极小值f(3)=2+6ln 3.
+6ln 2,在x=3处取得极小值f(3)=2+6ln 3.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷2练习卷(解析版) 题型:解答题
已知向量a=(Asin ωx,Acos ωx),b=(cos θ,sin θ),f(x)=a·b+1,其中A>0,ω>0,θ为锐角.f(x)的图象的两个相邻对称中心的距离为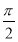 ,且当x=
,且当x=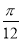 时,f(x)取得最大值3.
时,f(x)取得最大值3.
(1)求f(x)的解析式;
(2)将f(x)的图象先向下平移1个单位,再向左平移φ(φ>0)个单位得g(x)的图象,若g(x)为奇函数,求φ的最小值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练x4-1练习卷(解析版) 题型:填空题
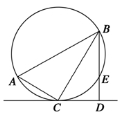
如图,在△ABC中,∠C=90°,∠A=60°,AB=20,过C作△ABC的外接圆的切线CD,BD⊥CD,BD与外接圆交于点E,则DE的长为______.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练6练习卷(解析版) 题型:选择题
将函数y=sin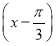 的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将所得图象向左平移
的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将所得图象向左平移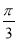 个单位,则所得函数图象对应的解析式为( ).
个单位,则所得函数图象对应的解析式为( ).
A.y=sin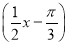 B.y=sin
B.y=sin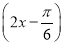
C.y=sin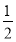 x D.y=sin
x D.y=sin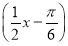
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练5练习卷(解析版) 题型:选择题
设函数f(x)满足x2f′(x)+2xf(x)=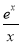 ,f(2)=
,f(2)=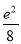 ,则x>0时,f(x)( ).
,则x>0时,f(x)( ).
A.有极大值,无极小值
B.有极小值,无极大值
C.既有极大值又有极小值
D.既无极大值也无极小值
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练4练习卷(解析版) 题型:填空题
设P为曲线C:f(x)=x2-x+1上的点,曲线C在点P处的切线斜率的取值范围是[-1,3],则点P的纵坐标的取值范围是________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练3练习卷(解析版) 题型:解答题
已知函数f(x)=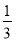 ax3-
ax3-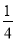 x2+cx+d(a,c,d∈R)满足f(0)=0,f′(1)=0,且f′(x)≥0在R上恒成立.
x2+cx+d(a,c,d∈R)满足f(0)=0,f′(1)=0,且f′(x)≥0在R上恒成立.
(1)求a,c,d的值;
(2)若h(x)=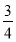 x2-bx+
x2-bx+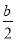 -
-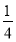 ,解不等式f′(x)+h(x)<0.
,解不等式f′(x)+h(x)<0.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练2练习卷(解析版) 题型:选择题
设函数f(x)=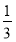 x-ln x(x>0),则y=f(x)( ).
x-ln x(x>0),则y=f(x)( ).
A.在区间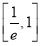 ,(1,e)内均有零点
,(1,e)内均有零点
B.在区间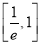 ,(1,e)内均无零点
,(1,e)内均无零点
C.在区间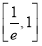 内有零点,在区间(1,e)内无零点
内有零点,在区间(1,e)内无零点
D.在区间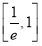 内无零点,在区间(1,e)内有零点
内无零点,在区间(1,e)内有零点
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习6-1直线与圆练习卷(解析版) 题型:选择题
已知直线l1:k1x+y+1=0与直线l2:k2x+y-1=0,那么“k1=k2”是“l1∥l2”的( ).
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com