
设函数f(x)=ax2+bx+b-1(a≠0).
(1)当a=1,b=-2时,求函数f(x)的零点;
(2)若对任意b∈R,函数f(x)恒有两个不同零点,求实数a的取值范围.
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷1练习卷(解析版) 题型:选择题
设m为正整数,(x+y)2m展开式的二项式系数的最大值为a,(x+y)2m+1展开式的二项式系数的最大值为b,若13a=7b,则m等于( ).
A.5 B.6 C.7 D.8
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练5练习卷(解析版) 题型:选择题
设函数f(x)满足x2f′(x)+2xf(x)=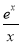 ,f(2)=
,f(2)=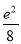 ,则x>0时,f(x)( ).
,则x>0时,f(x)( ).
A.有极大值,无极小值
B.有极小值,无极大值
C.既有极大值又有极小值
D.既无极大值也无极小值
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练3练习卷(解析版) 题型:解答题
已知函数f(x)=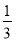 ax3-
ax3-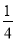 x2+cx+d(a,c,d∈R)满足f(0)=0,f′(1)=0,且f′(x)≥0在R上恒成立.
x2+cx+d(a,c,d∈R)满足f(0)=0,f′(1)=0,且f′(x)≥0在R上恒成立.
(1)求a,c,d的值;
(2)若h(x)=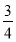 x2-bx+
x2-bx+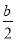 -
-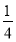 ,解不等式f′(x)+h(x)<0.
,解不等式f′(x)+h(x)<0.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练3练习卷(解析版) 题型:选择题
小王从甲地到乙地往返的时速分别为a和b(a<b),其全程的平均时速为v,则( ).
A.a<v< 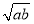 B.v=
B.v=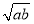
C. 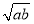 <v<
<v< 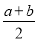 D.v=
D.v=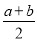
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练2练习卷(解析版) 题型:选择题
设函数f(x)=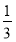 x-ln x(x>0),则y=f(x)( ).
x-ln x(x>0),则y=f(x)( ).
A.在区间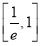 ,(1,e)内均有零点
,(1,e)内均有零点
B.在区间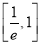 ,(1,e)内均无零点
,(1,e)内均无零点
C.在区间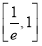 内有零点,在区间(1,e)内无零点
内有零点,在区间(1,e)内无零点
D.在区间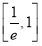 内无零点,在区间(1,e)内有零点
内无零点,在区间(1,e)内有零点
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练1练习卷(解析版) 题型:填空题
已知函数y=f(x)是R上的偶函数,对?x∈R都有f(x+4)=f(x)+f(2)成立.当x1,x2∈[0,2],且x1≠x2时,都有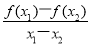 <0,给出下列命题:
<0,给出下列命题:
①f(2)=0;
②直线x=-4是函数y=f(x)图象的一条对称轴;
③函数y=f(x)在[-4,4]上有四个零点;
④f(2 014)=0.
其中所有正确命题的序号为________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习7-2随机变量及其分布练习卷(解析版) 题型:选择题
连续向一目标射击,直至击中为止,已知一次射击命中目标的概率为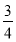 则射击次数为3的概率为( ).
则射击次数为3的概率为( ).
A.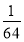 B.
B.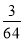 C.
C.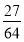 D.
D.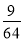
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习4-2数列求和与数列的综合应用练习卷(解析版) 题型:解答题
已知等差数列{an}的前n项和为Sn,n∈N*,且a2=3,点(10,S10)在直线y=10x上.
(1)求数列{an}的通项公式;
(2)设bn=2an+2n,求数列{bn}的前n项和Tn.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com