
如图,平面ABCD⊥平面ADEF,其中ABCD为矩形,ADEF为梯形,AF∥DE,AF⊥FE,AF=AD=2DE=2,M为AD的中点.
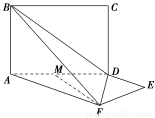
(1)证明:MF⊥BD;
(2)若二面角A-BF-D的平面角的余弦值为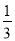 ,求AB的长.
,求AB的长.
(1)见解析 (2)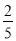
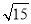
【解析】(1)证明 由已知得△ADF为正三角形,所以MF⊥AD,
因为平面ABCD⊥平面ADEF,平面ABCD∩平面ADEF=AD,
MF?平面ADEF,所以MF⊥BD.
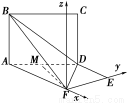
(2)设AB=x,以F为原点,AF,FE所在直线分别为x轴,y轴建立如图所示的空间直角坐标系,则F(0,0,0),A(-2,0,0),D(-1,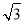 ,0),B(-2,0,x),所以
,0),B(-2,0,x),所以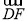 =(1,-
=(1,- ,0),
,0),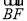 =(2,0,-x).
=(2,0,-x).
因为EF⊥平面ABF,所以平面ABF的法向量可取n1=(0,1,0).
设n2=(x1,y1,z1)为平面BFD的法向量,则
可取n2=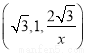 .
.
因为cos〈n1,n2〉=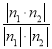 =
=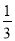 ,
,
得x=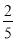
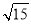 ,所以AB=
,所以AB=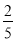
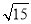 .
.


科目:高中数学 来源:2015届高考苏教数学(理)训练14 导数与函数单调性(解析版) 题型:解答题
已知函数f(x)=x+sin x.
(1)设P,Q是函数f(x)图像上相异的两点,证明:直线PQ的斜率大于0;
(2)求实数a的取值范围,使不等式f(x)≥axcos x在 上恒成立.
上恒成立.
查看答案和解析>>
科目:高中数学 来源:2015届高考苏教数学(理)训练1 集合(解析版) 题型:解答题
设集合A={x|x2+2x-3>0},B={x|x2-2ax-1≤0,a>0}.若A∩B中恰含有一个整数,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2015届高考苏教数学训练3 简单的逻辑联结词、全称量词与存在量词(解析版) 题型:填空题
若命题“?x∈R,ax2-ax-2≤0”是真命题,则实数a的取值范围是________.
查看答案和解析>>
科目:高中数学 来源:2015届高考苏教数学训练3 简单的逻辑联结词、全称量词与存在量词(解析版) 题型:填空题
若命题“?x∈R,使得x2+(a-1)x+1≤0”为假命题,则实数a的取值范围是________.
查看答案和解析>>
科目:高中数学 来源:2015届高考数学(理)一轮总复习专题突破四 高考立体几何(解析版) 题型:选择题
如图,在四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°,将△ABD沿BD折起,使平面ABD⊥平面BCD,构成三棱锥A-BCD,则在三棱锥A-BCD中,下列命题正确的是( )
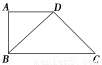
A.平面ABD⊥平面ABC B.平面ADC⊥平面BDC
C.平面ABC⊥平面BDC D.平面ADC⊥平面ABC
查看答案和解析>>
科目:高中数学 来源:2015届高考数学(理)一轮总复习专题突破六 高考概率与统计(解析版) 题型:选择题
已知x,y满足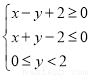 ,(x∈Z,y∈Z),每一对整数(x,y)对应平面上一个点,则过这些点中的其中3个点可作不同的圆的个数为( )
,(x∈Z,y∈Z),每一对整数(x,y)对应平面上一个点,则过这些点中的其中3个点可作不同的圆的个数为( )
A.45 B.36 C.30 D.27
查看答案和解析>>
科目:高中数学 来源:2015届高考数学(理)一轮总复习专题突破五 高考解析几何(解析版) 题型:填空题
已知l1:2x+my+1=0与l2:y=3x-1,若两直线平行,则m的值为________.
查看答案和解析>>
科目:高中数学 来源:2015届高考数学(理)一轮总复习专题突破一 高考函数与导数(解析版) 题型:选择题
与直线2x-6y+1=0垂直,且与曲线f(x)=x3+3x2-1相切的直线方程是( )
A.3x+y+2=0 B.3x-y+2=0
C.x+3y+2=0 D.x-3y-2=0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com