
(08年莆田四中一模理)(12分)
如图,在四棱锥![]() 中,底面
中,底面![]() 为矩形,
为矩形,![]() ⊥底面
⊥底面![]() ,
,![]() 是
是![]() 上一点.已知
上一点.已知![]() =
=![]() ,
,![]() ,
,![]() =
=![]()
(1)求证,![]() ⊥平面
⊥平面![]() ;
;
(2)求二面角![]() 的大小.
的大小.

解析:方法一:(1)在Rt△ADE中,AE=AD?tan![]()
![]() -----2分
-----2分
在Rt△ADE和Rt△EBC中,![]()
∴Rt△DAE∽Rt△EBC
∴∠ADE=∠EBC=![]() 又∠AED=
又∠AED=![]()
∴∠DEC=90°即DE⊥EC
又∵PD⊥平面ABCD ∴PD⊥CE
∴CE⊥平面PED --------- 6分
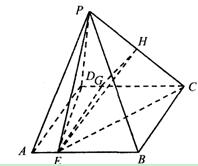
(2)过E作EG⊥CD交CD于G,作GH⊥PC交于PC于H,连结EH.
因PD⊥底面ABCD,所以PD⊥EG. 从而EG⊥平面PCD.
∵GH⊥PC,由三垂线定理得EH⊥PC
∴∠EHG为二面角E―PC―D的平面角 ---------10分
在△PDC中,PD=![]() ,CD=2,GC=
,CD=2,GC=![]()
由△PDC∽△GHC得GH=PD![]() 又EG=AD=
又EG=AD=![]()
∴在Rt△EHG中,GH=EG. ∴∠EHG=![]() ------12分
------12分
方法二:
(1) 以D为原点,![]() 分别为
分别为![]() 轴建立空间直角坐标系,
轴建立空间直角坐标系,
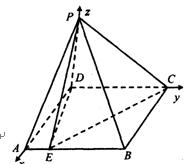
由已知可得
D(0,0,0),P(0,0,![]() ),C(0,2,0),A(
),C(0,2,0),A(![]() ,0,0)
,0,0)
B(![]() --------------2分
--------------2分
![]() -----4分
-----4分
![]() 即CE⊥DE,CE⊥DP ∴CE⊥平面PED (6分)
即CE⊥DE,CE⊥DP ∴CE⊥平面PED (6分)
(2)设平面PEC的法向量n(x,y,z) ------6分
则由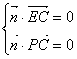 得
得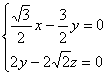
![]() 令
令![]() ,则
,则![]() )--10分
)--10分
∵AD⊥平面PDC ∴![]() 即为平面PDC的法向量
即为平面PDC的法向量

![]() 即二面角E―PC―D的大小为
即二面角E―PC―D的大小为![]() . ----12分
. ----12分


 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:高中数学 来源: 题型:
(08年莆田四中一模理) (14分)
由函数![]() 确定数列
确定数列![]() ,
,![]() ,若函数
,若函数![]() 的反函数
的反函数![]() 能确定数列
能确定数列![]() ,
,![]() ,则称数列
,则称数列![]() 是数列
是数列![]() 的“反数列”。
的“反数列”。
(1)若函数![]() 确定数列
确定数列![]() 的反数列为
的反数列为![]() ,求
,求![]() 的通项公式;
的通项公式;
(2)对(1)中![]() ,不等式
,不等式![]() 对任意的正整数
对任意的正整数![]() 恒成立,求实数
恒成立,求实数![]() 的范围;
的范围;
(3)设![]() ,若数列
,若数列![]() 的反数列为
的反数列为![]() ,
,![]() 与
与![]() 的公共项组成的数列为
的公共项组成的数列为![]() ;求数列
;求数列![]() 前
前![]() 项和
项和![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年莆田四中一模理)(12分)
某厂生产某种电子元件,如果生产出一件正品,可获利200元,如果生产出一件次品则损失100元.已
知该厂制造电子元件过程中,次品率![]() 与日产量
与日产量![]() 的函数关系是:
的函数关系是:![]() .
.
(1)将该厂的日盈利额![]() (元)表示为日产量
(元)表示为日产量![]() (件)的函数
(件)的函数![]() ;
;
(2)为获得最大盈利,该厂的日产量应为多少件?
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年莆田四中一模文)(12分)
已知等差数列![]() }的公差d大于0,且a2、a5是方程x2-12x+27=0的两根,数列
}的公差d大于0,且a2、a5是方程x2-12x+27=0的两根,数列![]() }的前n项和为Tn,
}的前n项和为Tn,
且![]()
(I)求数列![]() }、
}、![]() }的通项公式;
}的通项公式;
(II)记![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com