
某市职教中心组织厨师技能大赛,大赛依次设基本功(初赛)、面点制作(复赛)、热菜烹制(决赛)三个轮次的比赛,已知某选手通过初赛、复赛、决赛的概率分别是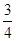 ,
,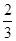 ,
,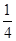 且各轮次通过与否相互独立.
且各轮次通过与否相互独立.
(I)设该选手参赛的轮次为 ,求
,求 的分布列和数学期望;
的分布列和数学期望;
(Ⅱ)对于(I)中的 ,设“函数
,设“函数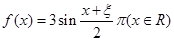 是偶函数”为事件D,求事件D发生的概率.
是偶函数”为事件D,求事件D发生的概率.
(I)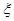 的分布列为:
的分布列为:
|
|
1 |
2 |
3 |
|
P |
|
|
|
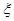 的数学期望
的数学期望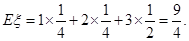
(Ⅱ)事件D发生的概率是 .
.
【解析】
试题分析:(I)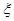 是否可以取0?每一选手必然能参加初赛,最多参加3场比赛,所以
是否可以取0?每一选手必然能参加初赛,最多参加3场比赛,所以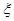 的取值为1,2,3.
的取值为1,2,3.
由于各轮次通过与否相互独立,所以用独立事件同时发生的概率公式便求得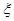 每个取值的概率,从而得分布列和期望.
每个取值的概率,从而得分布列和期望.
(Ⅱ)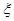 可以取1、2、3三个值,将这三个值代入函数式可知,.当
可以取1、2、3三个值,将这三个值代入函数式可知,.当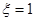 和
和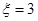 时,
时,
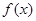 为偶函数.
为偶函数. 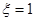 和
和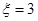 表示的事件是互斥的,所以由互斥事件的概率公式知,将这两个事件的概率相加,即得事件D发生的概率是.
表示的事件是互斥的,所以由互斥事件的概率公式知,将这两个事件的概率相加,即得事件D发生的概率是.
试题解析:(I)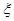 可能取值为1,2,3.
2分
可能取值为1,2,3.
2分
记“该选手通过初赛”为事件A,“该选手通过复赛”为事件B,
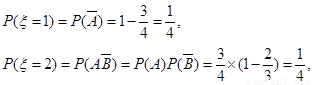
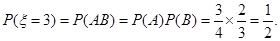 5分
5分
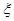 的分布列为:
的分布列为:
|
|
1 |
2 |
3 |
|
P |
|
|
|
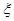 的数学期望
的数学期望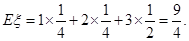 7分
7分
(Ⅱ)当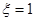 时,
时,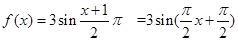
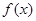 为偶函数;
为偶函数;
当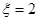 时,
时,
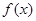 为奇函数;
为奇函数;
当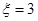 时,
时,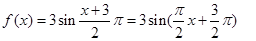
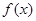 为偶函数;
为偶函数;
∴事件D发生的概率是 .
12分
.
12分
考点:随机变量的分布列及期望.


 灵星计算小达人系列答案
灵星计算小达人系列答案科目:高中数学 来源: 题型:
| 3 |
| 4 |
| 2 |
| 3 |
| 1 |
| 4 |
| x+ξ |
| 2 |
查看答案和解析>>
科目:高中数学 来源:威海模拟 题型:解答题
| 3 |
| 4 |
| 2 |
| 3 |
| 1 |
| 4 |
| x+ξ |
| 2 |
查看答案和解析>>
科目:高中数学 来源:山东省模拟题 题型:解答题
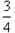 ,
,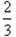 ,
,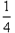 且各轮次通过与否相互独立.
且各轮次通过与否相互独立.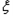 ,求
,求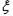 的分布列和数学期望;
的分布列和数学期望; 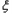 ,设
,设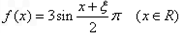 是偶函数D,求事件D发生的概率.
是偶函数D,求事件D发生的概率.查看答案和解析>>
科目:高中数学 来源:2012-2013学年福建省泉州市晋江市季延中学高二(下)期末数学试卷(理科)(解析版) 题型:解答题
 ,
, ,
, 且各轮次通过与否相互独立.
且各轮次通过与否相互独立.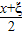 π(x∈R)是偶函数”为事件D,求事件D发生的概率.
π(x∈R)是偶函数”为事件D,求事件D发生的概率.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com