
分析 根据锐角△ABC和∠B=2∠A求出∠C,列出不等式组求出A的范围,根据正弦定理及二倍角的正弦公式化简,根据余弦函数单调性求出|AC|的取值范围.
解答 解:∵△ABC是锐角三角形,且∠B=2∠A,
∴∠C=π-∠A-∠B=π-3∠A,则$\left\{\begin{array}{l}{0<2∠A<\frac{π}{2}}\\{0<π-3∠A<\frac{π}{2}}\end{array}\right.$,
解得$\frac{π}{6}<∠A<\frac{π}{4}$,
又|BC|=$\frac{1}{2}$,由正弦定理得$\frac{|BC|}{sin∠A}=\frac{|AC|}{sin∠B}$,
∴$\frac{\frac{1}{2}}{sin∠A}=\frac{|AC|}{2sin∠Acos∠A}$,得|AC|=cos∠A,
∴|AC|的取值范围是$(\frac{\sqrt{2}}{2},\frac{\sqrt{3}}{2})$,
故答案为:$(\frac{\sqrt{2}}{2},\frac{\sqrt{3}}{2})$.
点评 本题考查了正弦定理,以及二倍角的正弦公式化简求值,解题关键是根据锐角三角形、内角和定理求出角的范围.


 高中必刷题系列答案
高中必刷题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 24种 | B. | 96种 | C. | 72种 | D. | 48种 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
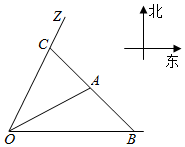 为了寻找马航MH370残骸,我国“雪龙号”科考船于2014年3月26日从港口O出发,沿北偏东15°角的射线OZ方向航行,而在港口北偏东60°角的方向上有一个给科考船补给物资的小岛A,OA=100(1+$\sqrt{3}$)海里,现指挥部需要紧急征调位于港口O正东x(x>200)海里的B处的补给船,速往小岛A装上补给物资供给科考船,该船沿BA方向全速追赶科考船,并在C相遇,经测算当两船运行的航线与海岸线OB围成的三角形OBC的面积S小时,这种补给方案最优.
为了寻找马航MH370残骸,我国“雪龙号”科考船于2014年3月26日从港口O出发,沿北偏东15°角的射线OZ方向航行,而在港口北偏东60°角的方向上有一个给科考船补给物资的小岛A,OA=100(1+$\sqrt{3}$)海里,现指挥部需要紧急征调位于港口O正东x(x>200)海里的B处的补给船,速往小岛A装上补给物资供给科考船,该船沿BA方向全速追赶科考船,并在C相遇,经测算当两船运行的航线与海岸线OB围成的三角形OBC的面积S小时,这种补给方案最优.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com