
【题目】越野汽车轮胎的质量是根据其正常使用的时间来衡量,使用时间越长,表明质量越好,且使用时间大于或等于6千小时的为优质品.现用![]() ,
,![]() 两种不同型号的汽车轮胎做试验,各随机抽取部分产品作为样本,得到试验结果的频率分布直方图如图所示,以上述试验结果中各组的频率作为相应的概率.
两种不同型号的汽车轮胎做试验,各随机抽取部分产品作为样本,得到试验结果的频率分布直方图如图所示,以上述试验结果中各组的频率作为相应的概率.

(1)现从大量的![]() ,
,![]() 两种型号的轮胎中各随机抽取2件产品,求其中至少有3件是优质品的概率;
两种型号的轮胎中各随机抽取2件产品,求其中至少有3件是优质品的概率;
(2)通过多年统计发现,![]() 型轮胎每件产品的利润
型轮胎每件产品的利润![]() (单位:元)与其使用时间
(单位:元)与其使用时间![]() (单位:千小时)的关系如下表:
(单位:千小时)的关系如下表:
使用时间 |
|
|
|
每件产品的利润 |
| 200 | 400 |
若从大量的![]() 型轮胎中随机抽取两件,其利润之和记为
型轮胎中随机抽取两件,其利润之和记为![]() (单位:元),求
(单位:元),求![]() 的分布列及数学期望.
的分布列及数学期望.
【答案】(1)![]() ;(2)分布列见解析,
;(2)分布列见解析,![]()
【解析】
(1)先根据直方图得到抽取一件![]() 和一件
和一件![]() 型轮胎为优质品的概率,再根据互斥事件的加法公式和独立事件的乘法公式可得结果;
型轮胎为优质品的概率,再根据互斥事件的加法公式和独立事件的乘法公式可得结果;
(2)据题意知,![]() 的可能取值为
的可能取值为![]() ,0,200,400,600,800.根据概率公式求出
,0,200,400,600,800.根据概率公式求出![]() 的各个取值的概率,再写出分布列,根据数学期望公式求出数学期望即可.
的各个取值的概率,再写出分布列,根据数学期望公式求出数学期望即可.
(1)由直方图可知,从![]() 型号轮胎中随机抽取一件产品为优质品的概率
型号轮胎中随机抽取一件产品为优质品的概率![]() ,
,
从![]() 型轮胎中随机抽取一件产品为优质品的概率
型轮胎中随机抽取一件产品为优质品的概率![]() ,
,
所以从![]() ,
,![]() 两种型号轮胎中各随机抽取2件产品,其中至少有3件是优质品的概率
两种型号轮胎中各随机抽取2件产品,其中至少有3件是优质品的概率
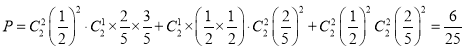 .
.
(2)据题意知,![]() 的可能取值为
的可能取值为![]() ,0,200,400,600,800.
,0,200,400,600,800.
所以![]() ,
,![]() ,
,
![]() ,
,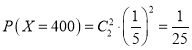 ,
,
![]() ,
,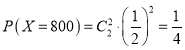 ,
,
那么![]() 的分布列为
的分布列为
|
| 0 | 200 | 400 | 600 | 800 |
|
|
|
|
|
|
|
则数学期望![]() .
.


 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a1=![]() ,an+1=3an-1(n∈N*).
,an+1=3an-1(n∈N*).
(1)若数列{bn}满足bn=an-![]() ,求证:{bn}是等比数列;
,求证:{bn}是等比数列;
(2)求数列{an}的前n项和Sn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场一年购进某种货物900吨,每次都购进x吨,运费为每次9万元,一年的总存储费用为![]() 万元
万元
(1)要使一年的总运费与总存储费用之和最小,则每次购买多少吨?
(2)要使一年的总运费与总存储费用之和不超过585万元,则每次购买量在什么范围?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥P﹣ABCD中,四边形ABCD是菱形,∠BAD=60°,又PD⊥平面ABCD,点E是棱AD的中点,F在棱PC上,且AD=PD=4.

(1)证明:平面BEF⊥平面PAD;
(2)若PA∥平面BEF,求四棱锥F﹣BCDE的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱拄![]() 中,
中,![]() 侧面
侧面![]() ,已知
,已知![]() ,
,![]() ,
,![]() .
.

(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)试在棱![]() (不包含端点
(不包含端点![]() )上确定一点
)上确定一点![]() 的位置,使得
的位置,使得![]() ;
;
(Ⅲ)在(Ⅱ)的条件下,求![]() 和平面
和平面![]() 所成角正弦值的大小.
所成角正弦值的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() .
.
(1)若展开式中奇数项的二项式系数和为128,求展开式中二项式系数最大的项的系数;
(2)若展开式前三项的二项式系数和等于37,求展开式中系数最大的项.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在空间中,给出下列说法:①平行于同一个平面的两条直线是平行直线;②垂直于同一条直线的两个平面是平行平面;③若平面![]() 内有不共线的三点到平面
内有不共线的三点到平面![]() 的距离相等,则
的距离相等,则![]() ;④过平面
;④过平面![]() 的一条斜线,有且只有一个平面与平面
的一条斜线,有且只有一个平面与平面![]() 垂直.其中正确的是( )
垂直.其中正确的是( )
A. ①③B. ②④C. ①④D. ②③
查看答案和解析>>
科目:高中数学 来源: 题型:
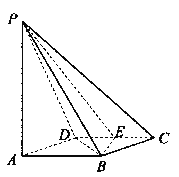
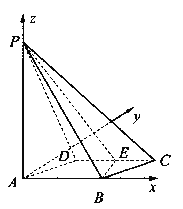
【题目】如图所示,四棱锥![]() 的底面
的底面![]() 是边长为1的菱形,
是边长为1的菱形,![]() ,
,
E是CD的中点,PA![]() 底面ABCD,
底面ABCD,![]() .
.
(I)证明:平面PBE![]() 平面PAB;
平面PAB;
(II)求二面角A—BE—P和的大小.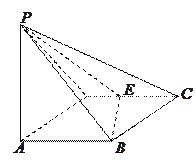
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com