在等差数列{an}中,已知a1=20,前n项和为Sn,且S10=S15,
(Ⅰ)求{an}的通项公式;
(Ⅱ)求{an}的前n项和Sn及使得Sn最大的序号n的值.
解:(1)由题意可知:
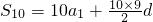
,

∵a
1=20,S
10=S
15即10a
1+45d=15a
1+105d
解得:
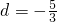
∴
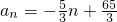
;(6分)
(2)由(1)知S
n=na
1+

d=

因为
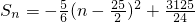
所以n=12,13时,S
n取得最大值.(12分)
分析:(1)设等差数列的公差为d,由首项a
1的值,利用等差数列的求和公式化简S
10=S
15,即可求出公差d的值,由首项a
1和d的值,写出等差数列{a
n}的通项公式即可;
(2)由(1)求出的公差d和首项a
1,根据等差数列的前n项和公式表示出S
n,配方后,根据二次函数求最大值的方法,即可求出S
n最大时序号n的值.
点评:此题考查了等差数列的通项公式,前n项和公式以及数列的函数特征.学生在求S
n取得最大值时n值时,注意n为正整数这个条件.

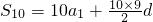 ,
,
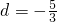
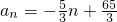 ;(6分)
;(6分) d=
d=
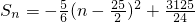


 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案