
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,
,![]() ,
,![]() ,且当
,且当![]() 时,
时,![]() 与6的等差中项为
与6的等差中项为![]() .数列
.数列![]() 为等比数列,且
为等比数列,且![]() ,
,![]() .
.
(Ⅰ)求数列![]() 、
、![]() 的通项公式;
的通项公式;
(Ⅱ)求数列![]() 的前
的前![]() 项和
项和![]() .
.
【答案】见解析
【解析】(Ⅰ)由已知当![]() 时,
时,![]() ,整理得
,整理得![]() ,
,
所以数列![]() 从第2项起构成等差数列,公差
从第2项起构成等差数列,公差![]() .
.
而![]() ,
,
故当![]() 时,
时,![]() . ----------------------2分
. ----------------------2分
而![]() ,显然
,显然![]() ,
,
故![]() . ------------------4分
. ------------------4分
等比数列![]() 中,
中,![]() ,
,![]() ,故其公比
,故其公比![]() .
.
所以其通项![]() . ---------------------------6分
. ---------------------------6分
(Ⅱ)令![]() ,由(Ⅰ)知,
,由(Ⅰ)知,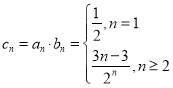 . ---------------7分
. ---------------7分
当![]() 时,
时,![]() .
.
当![]() 时,
时,![]()
![]() ①
①
![]() ②
②
①![]() ②,得
②,得
![]()
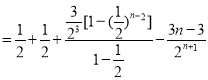
![]()
![]() ,
,
所以![]() . -------------------11分
. -------------------11分
显然,当![]() 时,也成立.
时,也成立.
故![]() . -------------------12分
. -------------------12分
【命题意图】本题考查![]() 与
与![]() 的关系、等比数列的基本运算、数列通项公式以及数列求和等,考查基本的运算能力与逻辑推理能力等.
的关系、等比数列的基本运算、数列通项公式以及数列求和等,考查基本的运算能力与逻辑推理能力等.


科目:高中数学 来源: 题型:
【题目】如图,海中有一小岛,周围3.8海里内有暗礁.一军舰从A地出发由西向东航行,望见小岛B在北偏东75°,航行8海里到达C处,望见小岛B在北偏东60°.若此舰不改变舰行的方向继续前进,问此舰有没有触礁的危险?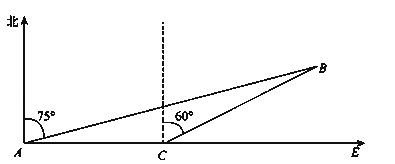
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】面对全球范围内日益严峻的能源形势与环保压力,环保与低碳成为今后汽车发展的一大趋势,越来越多的消费者对新能源汽车表示出更多的关注,某研究机构从汽车市场上随机抽取N辆纯电动汽车调查其续航里程(单次充电后能行驶的最大里程),被调查汽车的续航里程全部介于100公里和450公里之间,根据调查数据形成了如图所示频率分布表及频率分布直方图.
频率分布表
分组 | 频数 | 频率 |
[100,150) | 1 | 0.05 |
[150,200) | 3 | 0.15 |
[200,250) | x | 0.1 |
[250,300) | 6 | 0.3 |
[300,350) | 4 | 0.2 |
[350,400) | 3 | y |
[400,450] | 1 | 0.05 |
合计 | N | 1 |
(1)试确定频率分布表中x,y,N的值,并补全频率分布直方图;
(2)若从续航里程在[200,250)及[350,400)的车辆中随机抽取2辆车,求两辆车续航里程都在[350,400)的概率.
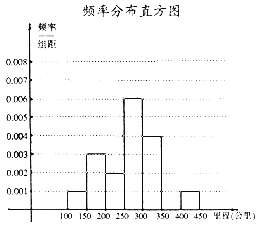
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,且过点
,且过点![]() .
.

(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)已知椭圆的左焦点为![]() ,直线
,直线![]() 与椭圆
与椭圆![]() 交于不同两点
交于不同两点![]() ,
,![]() (
(![]() 都在
都在![]() 轴上方),且
轴上方),且![]() .
.
(ⅰ)若点![]() 的横坐标为1,求
的横坐标为1,求![]() 的面积;
的面积;
(ⅱ)直线![]() 是否恒过定点?若过定点,求出该定点的坐标;若不过定点,请说明理由.
是否恒过定点?若过定点,求出该定点的坐标;若不过定点,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某社区为丰富居民节日活动,组织了“迎新春”象棋大赛,已知由1,2,3号三位男性选手和4,5号两位女性选手组成混合组参赛.已知象棋大赛共有三轮,设三位男性选手在一至三轮胜出的概率依次是![]() ;两名女性选手在一至三轮胜出的概率依次是
;两名女性选手在一至三轮胜出的概率依次是![]() .
.
(Ⅰ)若该组五名选手与另一组选手进行小组淘汰赛,每名选手只比赛一局,共五局比赛,求该组两名女性选手的比赛次序恰好不相邻的概率;
(Ⅱ)若一位男性选手因身体不适退出比赛,剩余四人参加个人比赛,比赛结果相互不影响,设![]() 表示该组选手在四轮中胜出的人数,求随机变量
表示该组选手在四轮中胜出的人数,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4—4:坐标系与参数方程
已知直线l经过点![]() ,倾斜角
,倾斜角![]() ,圆
,圆![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)写出直线l的参数方程,并把圆![]() 的方程化为直角坐标方程;
的方程化为直角坐标方程;
(Ⅱ)设l与圆![]() 相交于
相交于![]() 两点,求点
两点,求点![]() 到
到![]() 两点的距离之积.
两点的距离之积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场举行节日促销活动,消费满一定数额即可获得一次抽奖机会,抽奖这可以从以下两种方式中任选一种进行抽奖.
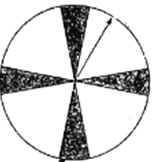
抽奖方式①:让抽奖者随意转动如图所示的圆盘,圆盘停止后指针指向阴影部分(图中四个阴影部分均为扇形,且每个扇形圆心角均为![]() ,边界忽略不计)即中奖.
,边界忽略不计)即中奖.
抽奖方式②:让抽奖者从装有3个白球和3个红球的盒子中一次性摸出2个球(球除颜色外不加区分),如果摸到的是2个红球,即中奖.
假如你是抽奖者,为了让中奖的可能性大,你应该选择哪一种抽奖方式?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)是定义在R上的奇函数,且当x≥0时, ![]() ,若存在x∈[t2﹣1,t],使不等式f(2x+t)≥2f(x)成立,则实数t的取值范围是. .
,若存在x∈[t2﹣1,t],使不等式f(2x+t)≥2f(x)成立,则实数t的取值范围是. .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设a为实数,记函数f(x)=a ![]() +
+ ![]() +
+ ![]() 的最大值为g(a).
的最大值为g(a).
(1)设t= ![]() +
+ ![]() ,求t的取值范围,并把f(x)表示为t的函数m(t);
,求t的取值范围,并把f(x)表示为t的函数m(t);
(2)求g(a);
(3)试求满足g(a)=g( ![]() )的所有实数a.
)的所有实数a.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com