②③④
分析:题目给出的是新定义题,定义的“好区间”是指的如果存在一个区间M=[a,b],使得以该区间为定义域的前提下,函数的值域也是该区间.
①对于函数f(x)=sinx,根据其在

上是单调增函数,通过分析方程sinx=x在

上仅有一解,在定义域其它范围内无解说明函数没有“好区间”;
②通过分析函数f(x)=|2
x-1|的图象,知函数在[0,+∞)上是增函数,在该范围内取x∈[0,1]时,对应的函数值的范围也是[0,1],说明区间[0,1]是函数的一个好区间;
③通过对已知函数求导,分析出函数的单调区间,找到极大值点和极小值点,并求出极大值b和极小值a,而求得的
f(a)与f(b)在[a,b]范围内,所以[a,b]为该函数的一个“好区间”;
④根据函数在定义域内是单调函数,函数若有“好区间”,则方程f(x)=x应有两根,利用函数单调性,结合根的存在性定理判断即可.
解答:①函数f(x)=sinx在

上是单调增函数,若函数在

上存在“好区间”[a,b],
则必有sina=a,sinb=b.
即方程sinx=x有两个根,令g(x)=sinx-x,g
′(x)=cosx-1≤0在

上恒成立,
所以函数g(x)在

上为减函数,则函数g(x)=sinx-x在

上至多有一个零点,
即方程sinx=x在

上不可能有两个解,又因为f(x)的值域为[-1,1],所以当x<

或x>

时,
方程sinx=x无解.
所以函数f(x)=sinx没有“好区间”;
②对于函数f(x)=|2
x-1|,该函数在[0,+∞)上是增函数,由幂函数的性质我们易得,M=[0,1]时,
f(x)∈[0,1]=M,所以M=[0,1]为函数f(x)=|2
x-1|的一个“好区间”;
③对于函数f(x)=x
3-3x,f
′(x)=3x
2-3=3(x-1)(x+1).
当x∈(-1,1)时,f
′(x)0.
所以函数f(x)=x
3-3x的增区间是(-∞,-1),(1,+∞),减区间是(-1,1).
取M=[-2,2],此时f(-2)=-2,f(-1)=2,f(1)=-2,f(2)=2.
所以函数f(x)=x
3-3x在M=[-2,2]上的值域也为[-2,2],则M=[-2,2]为函数的一个“好区间”;
④函数f(x)=lgx+1在定义域(0,+∞)上为增函数,若有“好区间”
则lga+1=a,lgb+1=b,也就是函数g(x)=lgx-x+1有两个零点.
显然x=1是函数的一个零点,
由
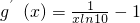
<0,得x>
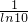
,函数g(x)在
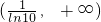
上为减函数;
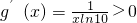
,得x<
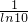
.函数在(0,
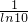
)上为增函数.
所以g(x)的最大值为g(
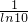
)>g(1)=0,
则该函数g(x)在(0,
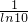
)上还有一个零点.
所以函数f(x)=lgx+1存在“好区间”.
故答案为②③④.
点评:本题是新定义题,考查了函数的定义域与值域的关系,体现了数学转化思想,此题中单调函数存在好区间的条件是f(x)=x,正确理解“好区间”的定义是解答该题的关键,是中档题.

 上是单调增函数,通过分析方程sinx=x在
上是单调增函数,通过分析方程sinx=x在 上仅有一解,在定义域其它范围内无解说明函数没有“好区间”;
上仅有一解,在定义域其它范围内无解说明函数没有“好区间”; 上是单调增函数,若函数在
上是单调增函数,若函数在 上存在“好区间”[a,b],
上存在“好区间”[a,b], 上恒成立,
上恒成立, 上为减函数,则函数g(x)=sinx-x在
上为减函数,则函数g(x)=sinx-x在 上至多有一个零点,
上至多有一个零点, 上不可能有两个解,又因为f(x)的值域为[-1,1],所以当x<
上不可能有两个解,又因为f(x)的值域为[-1,1],所以当x< 或x>
或x> 时,
时,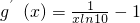 <0,得x>
<0,得x>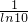 ,函数g(x)在
,函数g(x)在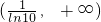 上为减函数;
上为减函数;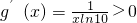 ,得x<
,得x<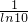 .函数在(0,
.函数在(0,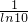 )上为增函数.
)上为增函数.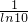 )>g(1)=0,
)>g(1)=0,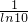 )上还有一个零点.
)上还有一个零点.
