
【题目】已知![]() 都是各项不为零的数列,且满足
都是各项不为零的数列,且满足![]() 其中
其中![]() 是数列
是数列![]() 的前
的前![]() 项和,
项和,![]() 是公差为
是公差为![]() 的等差数列.
的等差数列.
(1)若数列![]() 是常数列,
是常数列,![]() ,
,![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(2)若![]()
![]() 是不为零的常数),求证:数列
是不为零的常数),求证:数列![]() 是等差数列;
是等差数列;
(3)若![]() (
(![]() 为常数,
为常数,![]() ),
),![]() .求证:对任意
.求证:对任意![]() 的恒成立.
的恒成立.
【答案】(1)![]() ;(2)详见解析;(3)详见解析.
;(2)详见解析;(3)详见解析.
【解析】
(1)根据![]() ,
,![]() 可求得
可求得![]() ,再根据
,再根据![]() 是常数列代入
是常数列代入![]() 根据通项与前
根据通项与前![]() 项和的关系求解
项和的关系求解![]() 即可.
即可.
(2)取![]() ,并结合通项与前
,并结合通项与前![]() 项和的关系可求得
项和的关系可求得![]() 再根据
再根据![]() 化简可得
化简可得![]() ,代入
,代入![]() 化简即可知
化简即可知![]() ,再证明
,再证明![]() 也成立即可.
也成立即可.
(3)由(2) 当![]() 时,
时,![]() ,代入所给的条件化简可得
,代入所给的条件化简可得![]()
![]() ,进而证明可得
,进而证明可得![]() ,即数列
,即数列![]() 是等比数列.继而求得
是等比数列.继而求得![]() ,再根据作商法证明
,再根据作商法证明![]() 即可.
即可.
![]() 解:
解:![]()
![]() .
.
![]() 是各项不为零的常数列,
是各项不为零的常数列,
![]()
则![]() ,
,
则由![]() ,
,
及![]() 得
得![]() ,
,
当![]() 时,
时,![]() ,
,
两式作差,可得![]() .
.
当![]() 时,
时,![]() 满足上式,
满足上式,
则![]() ;
;
![]() 证明:
证明:![]() ,
,
当![]() 时,
时,![]() ,
,
两式相减得:![]()
即![]() .
.
即![]() .
.
又![]() ,
,
![]() ,
,
即![]() .
.
![]() 当
当![]() 时,
时,![]() ,
,
两式相减得:![]() .
.
![]() 数列
数列![]() 从第二项起是公差为
从第二项起是公差为![]() 的等差数列.
的等差数列.
又当![]() 时,由
时,由![]() 得
得![]() ,
,
当![]() 时,由
时,由![]() ,得
,得![]() .
.
故数列![]() 是公差为
是公差为![]() 的等差数列;
的等差数列;
![]() 证明:由
证明:由![]() ,当
,当![]() 时,
时,
![]() ,即
,即![]() ,
,
![]() ,
,
![]() ,即
,即![]() ,
,
![]() 即
即![]()
![]() ,
,
当![]() 时,
时,![]() 即
即![]() .
.
故从第二项起数列![]() 是等比数列,
是等比数列,
![]() 当
当![]() 时,
时,![]() .
.
![]() .
.
另外,由已知条件可得![]() ,
,
又![]() ,
,
![]() ,
,
因而![]() .
.
令![]() ,
,
则![]() .
.
故对任意的![]()
![]() 恒成立.
恒成立.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知直线![]() 的参数方程为
的参数方程为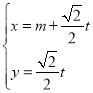 (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,且曲线
,且曲线![]() 的左焦点
的左焦点![]() 在直线
在直线![]() 上.
上.
(Ⅰ)求![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的参数方程;
的参数方程;
(Ⅱ)求曲线![]() 的内接矩形的周长的最大值.
的内接矩形的周长的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中AD∥BC,DA⊥AB,AD=2,AB=BC=1,CD![]() ,点E为PD中点.
,点E为PD中点.
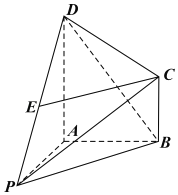
(1)求证:CE∥平面PAB;
(2)若PA=2,PD=2![]() ,∠PAB
,∠PAB![]() ,求平面PBD与平面ECD所成锐二面角的余弦值.
,求平面PBD与平面ECD所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,圆台![]() 的轴截面为等腰梯形
的轴截面为等腰梯形![]() ,
,![]() ,
,![]() ,
,![]() ,圆台
,圆台![]() 的侧面积为
的侧面积为![]() .若点C,D分别为圆
.若点C,D分别为圆![]() ,
,![]() 上的动点且点C,D在平面
上的动点且点C,D在平面![]() 的同侧.
的同侧.
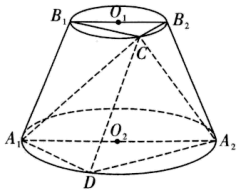
(1)求证:![]() ;
;
(2)若![]() ,则当三棱锥
,则当三棱锥![]() 的体积取最大值时,求多面体
的体积取最大值时,求多面体![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】改革开放以来,中国快递行业持续快速发展,快递业务量从上世纪![]() 年代的
年代的![]() 万件提升到2018年的
万件提升到2018年的![]() 亿件,快递行业的发展也给我们的生活带来了很大便利.已知某市某快递点的收费标准为:首重(重量小于等于
亿件,快递行业的发展也给我们的生活带来了很大便利.已知某市某快递点的收费标准为:首重(重量小于等于![]() )收费
)收费![]() 元,续重
元,续重![]() 元
元![]() (不足
(不足![]() 按
按![]() 算). (如:一个包裹重量为
算). (如:一个包裹重量为![]() 则需支付首付
则需支付首付![]() 元,续重
元,续重![]() 元,一共
元,一共![]() 元快递费用)
元快递费用)
(1)若你有三件礼物![]() 重量分别为
重量分别为![]() ,要将三个礼物分成两个包裹寄出(如:
,要将三个礼物分成两个包裹寄出(如:![]() 合为一个包裹,
合为一个包裹,![]() 一个包裹),那么如何分配礼物,使得你花费的快递费最少?
一个包裹),那么如何分配礼物,使得你花费的快递费最少?
(2)为了解该快递点2019年的揽件情况,在2019年内随机抽查了![]() 天的日揽收包裹数(单位:件),得到如下表格:
天的日揽收包裹数(单位:件),得到如下表格:
包裹数(单位:件) |
|
|
|
|
天数(天) |
|
|
|
|
现用这![]() 天的日揽收包裹数估计该快递点2019年的日揽收包裏数.若从2019年任取
天的日揽收包裹数估计该快递点2019年的日揽收包裏数.若从2019年任取![]() 天,记这
天,记这![]() 天中日揽收包裹数超过
天中日揽收包裹数超过![]() 件的天数为随机变量
件的天数为随机变量![]() 求
求![]() 的分布列和期望
的分布列和期望
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年5月20日以来,广东自西北到东南出现了一次明显降雨.为了对某地的降雨情况进行统计,气象部门对当地20日~28日9天内记录了其中100小时的降雨情况,得到每小时降雨情况的频率分布直方图如下:

若根据往年防汛经验,每小时降雨量在![]() 时,要保持二级警戒,每小时降雨量在
时,要保持二级警戒,每小时降雨量在![]() 时,要保持一级警戒.
时,要保持一级警戒.
(1)若以每组的中点代表该组数据值,求这100小时内每小时的平均降雨量;
(2)若从记录的这100小时中按照警戒级别采用分层抽样的方法抽取10小时进行深度分析.再从这10小时中随机抽取3小时,求抽取的这3小时中属于一级警戒时间的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知直线
中,已知直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数).在以坐标原点
为参数).在以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴,且与直角坐标系长度单位相同的极坐标系中,曲线
轴的正半轴为极轴,且与直角坐标系长度单位相同的极坐标系中,曲线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(1)求直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() .若直
.若直![]() 与曲线
与曲线![]() 相交于两点
相交于两点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)已知椭圆![]()
![]() (
(![]() )的半焦距为
)的半焦距为![]() ,原点
,原点![]() 到经过两点
到经过两点![]() ,
,![]() 的直线的距离为
的直线的距离为![]() .
.
(Ⅰ)求椭圆![]() 的离心率;
的离心率;
(Ⅱ)如图,![]() 是圆
是圆![]()
![]() 的一条直径,若椭圆
的一条直径,若椭圆![]() 经过
经过![]() ,
,![]() 两点,求椭圆
两点,求椭圆![]() 的方程.
的方程.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com