练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知函数，为自然对数的底数.

    （1）求函数的极值点；

    （2）若对任意，都有，求常数的取值范围.

    【答案】（1）的极小值点为，无极大值点；（2）.

    【解析】

    （1）求出导数，根据导数的符号判断函数的单调性从而求得函数的极值点；（2）构造函数，求出导数判断函数单调性从而证明当时对任意的不等式恒成立即可.

    （1）求导得（）.

    由得；由得.

    所以在区间内单调递减，在区间内单调递增.

    故函数的极小值点为，无极大值点.

    （2）设函数，则

    ，其中.

    （i）当时，因为，则必然存在，使在区间内恒成立，所以在区间内单调递增.

    于是，这与题设矛盾，故舍去.

    （ii）当时，因为在区间内单调递减，

    所以，故在区间内单调递减，

    于是，从而在区间内单调递减，

    故对任意，都有，满足题意.

    综上所述，常数的取值范围是.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】设函数.

    （1）讨论函数的单调性；

    （2）若，不等式恒成立，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆：的上顶点为，右焦点为F，连结TF并延长与椭圆交于点S，且.

    （1）求椭圆的方程；

    （2）已知直线与x轴交于点M，过点M的直线AB与交于A、B两点，点P为直线上任意一点，设直线AB与直线交于点N，记PA，PB，PN的斜率分别为，，，则是否存在实数，使得恒成立？若是，请求出的值；若不是，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某控制器中有一个易损部件，现统计了30个该部件的使用寿命，结果如下（单位：小时）；

    710 721 603 615 760 742 841 591 590 721 718 750 760 713 709

    681 736 654 722 732 722 715 726 699 755 751 709 733 705 700

    （1）估计该部件的使用寿命达到一个月及以上的概率（一个月按30天计算）；

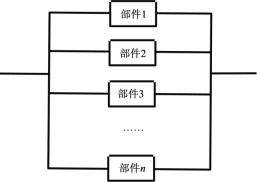
    （2）为了保证该控制器能稳定工作，将若干个同样的部件按下图连接在一起组成集成块，每一个部件是否能正常工作互不影响.对比和时，哪个能保证集成块使用寿命达到一个月及以上的概率超过0.8？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，倾斜角为的直线的参数方程为（其中为参数）.在以为极点、轴的非负半轴为极轴的极坐标系（两种坐标系的单位长度相同）中，曲线：的焦点的极坐标为.

    （1）求常数的值；

    （2）设与交于、两点，且，求的大小.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列图象中，可能是函数的图象的是( )

    A. B.

    C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，PO垂直圆O所在的平面，AB是圆O的一条直径，C为圆周上异于A，B的动点，D为弦BC的中点，，．

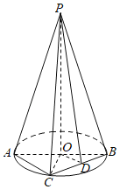
    （1）证明：平面平面；

    （2）当四面体PABC的体积最大时，求B到平面PAC的距离．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系xOy中，直线l的参数方程为（t为参数），以O为极点，x轴正半轴为极轴建立极坐标系，曲线C的极坐标方程为ρ（ρ﹣2sinθ）＝1．

    （1）求C的直角坐标方程；

    （2）设直线l与y轴相交于P，与曲线C相交于A、B两点，且|PA|+|PB|＝2，求点O到直线l的距离．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的左、右焦点分别为，点在椭圆上，且的面积为.

    （1）求椭圆的方程；

    （2）过原点作圆的两条切线，切点分别为，求.

    查看答案和解析>>

    同步练习册答案