
分析 (1)利用焦距,离心率,列出方程组,求解即可.
(2)设出P,求出MN,然后求解数量积推出结果即可.
解答 解:(1)$\left\{\begin{array}{l}c=4\\ \frac{b}{a}=\sqrt{3}\\{c^2}={a^2}+{b^2}\end{array}\right.⇒\left\{\begin{array}{l}a=2\\ b=2\sqrt{3}\end{array}\right.⇒\frac{x^2}{4}-\frac{y^2}{12}=1$
(2)$设P({x_0},{y_0}),{A_1}P:y=\frac{y_0}{{{x_0}+2}}(x+2),{A_2}P:y=\frac{y_0}{{{x_0}-2}}(x-2)$,
所以$M(1,\frac{{3{y_0}}}{{{x_0}+2}}),N(1,\frac{{-{y_0}}}{{{x_0}-2}})$,
所以$\overrightarrow{FM}•\overrightarrow{FN}=(-3,\frac{{3{y_0}}}{{{x_0}+2}})•(-3,\frac{{-{y_0}}}{{{x_0}-2}})=9-\frac{{3{y_0}^2}}{{{x_0}^2-4}}=9-\frac{{3{y_0}^2}}{{\frac{{{y_0}^2}}{3}}}=0$.
点评 本题考查椭圆的标准方程的应用,考查直线与椭圆位置关系的应用,考查计算能力.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
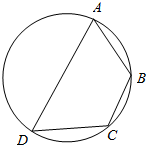 如图,已知四边形ABCD是圆内接四边形,且∠BCD=120°,AD=2,AB=BC=1.现有以下结论:
如图,已知四边形ABCD是圆内接四边形,且∠BCD=120°,AD=2,AB=BC=1.现有以下结论:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x>y | B. | x+y>0 | C. | x<y | D. | x2>y2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,+∞) | B. | $[\frac{1}{3},1]$ | C. | $[\frac{1}{3},+∞)$ | D. | (0,1] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com