
【题目】已知抛物线C:y2=2px(p>0)的焦点为F,点K(-1,0)为直线l与抛物线C准线的交点,直线l与抛物线C相交于A,B两点.
(1)求抛物线C的方程;
(2)设![]() ·
·![]() =
=![]() ,求直线l的方程.
,求直线l的方程.
【答案】(1)y2=4x(2)3x-4y+3=0或3x+4y+3=0.
【解析】
(1)由点K(﹣1,0)为直线l与抛物线C准线的交点知-![]() =-1,从而可求抛物线C的方程;(2)设直线l的方程,联立直线方程与抛物线方程,根据
=-1,从而可求抛物线C的方程;(2)设直线l的方程,联立直线方程与抛物线方程,根据![]() ·
·![]() =
=![]() ,结合韦达定理,即可求直线l的方程.
,结合韦达定理,即可求直线l的方程.
(1)依题意知-![]() =-1,解得p=2,所以抛物线C的方程为y2=4x.
=-1,解得p=2,所以抛物线C的方程为y2=4x.
(2)设A(x1,y1),B(x2,y2),且设直线l的方程为x=my-1(m≠0).
将x=my-1代入y2=4x,并整理,得y2-4my+4=0.
由Δ>0,得m2>1.从而y1+y2=4m,y1y2=4.
所以x1+x2=(my1-1)+(my2-1)=4m2-2,
x1x2=(my1-1)(my2-1)=m2y1y2-m(y1+y2)+1=1
因为![]() =(x1-1,y1),
=(x1-1,y1),![]() =(x2-1,y2),
=(x2-1,y2),
![]() ·
·![]() =(x1-1)(x2-1)+y1y2=x1x2-(x1+x2)+1+4=8-4m2,
=(x1-1)(x2-1)+y1y2=x1x2-(x1+x2)+1+4=8-4m2,
故8-4m2=![]() ,解得m=±
,解得m=±![]() 满足m2>1.
满足m2>1.
所以直线l的方程为x=±![]() y-1.
y-1.
即3x-4y+3=0或3x+4y+3=0.


 新思维寒假作业系列答案
新思维寒假作业系列答案科目:高中数学 来源: 题型:
【题目】某市举行“中学生诗词大赛”,分初赛和复赛两个阶段进行,规定:初赛成绩大于90分的具有复赛资格,某校有800名学生参加了初赛,所有学生的成绩均在区间![]() 内,其频率分布直方图如图.
内,其频率分布直方图如图.

(Ⅰ)求获得复赛资格的人数;
(Ⅱ)从初赛得分在区间![]() 的参赛者中,利用分层抽样的方法随机抽取
的参赛者中,利用分层抽样的方法随机抽取![]() 人参加学校座谈交流,那么从得分在区间
人参加学校座谈交流,那么从得分在区间![]() 与
与![]() 各抽取多少人?
各抽取多少人?
(Ⅲ)从(Ⅱ)抽取的![]() 人中,选出
人中,选出![]() 人参加全市座谈交流,设
人参加全市座谈交流,设![]() 表示得分在区间
表示得分在区间![]() 中参加全市座谈交流的人数,求
中参加全市座谈交流的人数,求![]() 的分布列及数学期望E(X).
的分布列及数学期望E(X).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解今年某校高三毕业班准备报考飞行员学生的体重情况,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1:2:3,其中第2小组的频数为15.
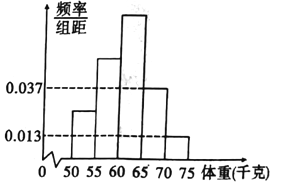
(1)求该校报考飞行员的总人数;
(2)以这所学校的样本数据来估计全省的总体数据,若从全省报考飞行员的同学中(人数很多)任选三人,设![]() 表示体重超过65公斤的学生人数,求
表示体重超过65公斤的学生人数,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 是定义在
是定义在![]() 上且满足如下条件的函数
上且满足如下条件的函数![]() 组成的集合:①对任意的
组成的集合:①对任意的![]() ,都有
,都有![]() ②存在常数
②存在常数![]() 使得对任意的
使得对任意的![]() ,都有
,都有![]() .
.
(1)设![]() 问
问![]() 是否属于
是否属于![]() ?说明理由;
?说明理由;
(2)若![]() 如果存在
如果存在![]() 使得
使得![]() 证明:这样的
证明:这样的![]() 是唯一的;
是唯一的;
(3)设![]() 且
且![]() 试求
试求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
袋中有形状和大小完全相同的四种不同颜色的小球,每种颜色的小球各有4个,分别编号为1,2,3,4.现从袋中随机取两个球.
(Ⅰ)若两个球颜色不同,求不同取法的种数;
(Ⅱ)在(1)的条件下,记两球编号的差的绝对值为随机变量X,求随机变量X的概率分布与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy 中,曲线C1的参数方程为:![]() (
(![]() ),M是
),M是![]() 上的动点,P点满足
上的动点,P点满足![]() ,P点的轨迹为曲线.
,P点的轨迹为曲线.![]()
(1)求![]() 的参数方程;
的参数方程;
(2)在以O为极点,x 轴的正半轴为极轴的极坐标系中,射线![]() 与
与![]() 的异于极点的交点为A,与
的异于极点的交点为A,与![]() 的异于极点的交点为B,求
的异于极点的交点为B,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】吸烟有害健康,远离烟草,珍惜生命。据统计一小时内吸烟5支诱发脑血管病的概率为0.02,一小时内吸烟10支诱发脑血管病的概率为0.16.已知某公司职员在某一小时内吸烟5支未诱发脑血管病,则他在这一小时内还能继吸烟5支不诱发脑血管病的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 不确定
D. 不确定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com