

(Ⅰ)证明:连结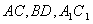 ,则O为AC,BD的交点,O1为A1C1, ,则O为AC,BD的交点,O1为A1C1,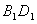 的交点。 的交点。 由平行六面体的性质知: 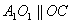 且 且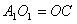 , ,∴四边形 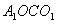 为平行四边形, 为平行四边形,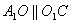 , ,又 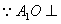 平面ABCD, 平面ABCD,∴ 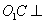 平面ABCD, 平面ABCD,又 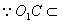 平面 平面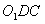 , ,∴平面 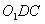 ⊥平面ABCD。 ⊥平面ABCD。 (Ⅱ)解:作EH⊥平面ABCD,垂足为H,则 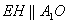 ,点H在直线AC上, ,点H在直线AC上,且EF在平面ABCD上的射影为HF。 由三垂线定理及其逆定理,知  , ,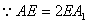 , ,∴AH=2HO,从而CH=2AH, 又 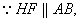 , ,∴CF=2BF,从而  , ,∴当F为BC的三等分点(靠近B)时,有EF⊥AD。 (Ⅲ)解:过点O作 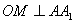 ,垂足为M,连接BM, ,垂足为M,连接BM, 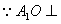 平面ABCD, 平面ABCD,∴ 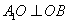 , ,又 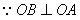 , ,∴OB⊥平面 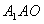 , ,由三垂线定理得 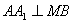 , ,∴∠OMB为二面角 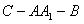 的平面角, 的平面角,在Rt△AMB中, 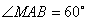 ,∴ ,∴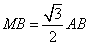 , ,又 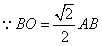 ,∴ ,∴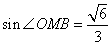 , ,∴ 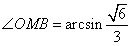 , ,即二面角的大小为 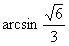 。 。 |
 |


科目:高中数学 来源: 题型:
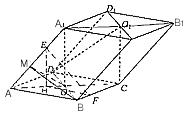
 如图,已知平行六面体ABC-A1B1C1的底面为正方形,O1,O分别为上、下底面中心,且A1在底面ABCD上的射影为O.
如图,已知平行六面体ABC-A1B1C1的底面为正方形,O1,O分别为上、下底面中心,且A1在底面ABCD上的射影为O.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知平行六面体ABCD-A1B1C1D1.
如图,已知平行六面体ABCD-A1B1C1D1.| A1M |
| MG |
| AB |
| AD |
| AA1 |
| A1M |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
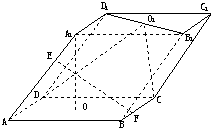 如图,已知平行六面体ABC-A1B1C1的底面为正方形,O1,O分别为上、下底面中心,且A1在底面ABCD上的射影为O.
如图,已知平行六面体ABC-A1B1C1的底面为正方形,O1,O分别为上、下底面中心,且A1在底面ABCD上的射影为O.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知平行六面体ABCD-A1B1C1D1.
如图,已知平行六面体ABCD-A1B1C1D1.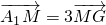 ,设
,设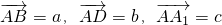 ,用向量a、b、c表示向量
,用向量a、b、c表示向量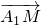 ;
;查看答案和解析>>
科目:高中数学 来源:2012-2013学年安徽省芜湖一中高二(上)期中数学试卷(文科)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com