
【题目】已知在正整数n的各位数字中,共含有![]() 个1,
个1,![]() 个2,,
个2,,![]() 个n.证明:
个n.证明:![]() 并确定使等号成立的条件.
并确定使等号成立的条件.
【答案】见解析
【解析】
对正整数n的位数使用数学归纳法.
当![]() 是一位数,即
是一位数,即![]() 时,所证式显然成立,
时,所证式显然成立,
这是因为,此时![]() 的十进制表达式中只有一位数字
的十进制表达式中只有一位数字![]() ,
,
即![]() ,其余
,其余![]() ,所以,左边=
,所以,左边=![]() =右边.
=右边.
假设当正整数![]() 不超过k位,即
不超过k位,即![]() 时,结论皆成立.
时,结论皆成立.
现考虑![]() 为
为![]() 位数,即
位数,即![]() 时的情形.
时的情形.
设![]() 的首位数字为r.则
的首位数字为r.则![]() . ①
. ①
若![]() ,则在数
,则在数![]() 的各位数字中,
的各位数字中,![]() ,其余
,其余![]() .
.
显然,![]() .
.
若![]() ,记
,记![]() 的各位数字中含有
的各位数字中含有![]() 个1,
个1,![]() 个2,…,
个2,…,![]() 个r,…,
个r,…,![]() 个9.
个9.
则![]() 的各位数字中,含有
的各位数字中,含有![]() 个r、
个r、![]() 个j
个j![]() .
.
注意到,正整数![]() 不超过k位.
不超过k位.
由归纳法假设,对![]() 有
有
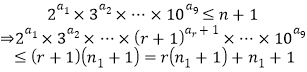
![]() ②
②
则当![]() 为
为![]() 位数时,结论也成立.
位数时,结论也成立.
故由数学归纳法,知对一切正整数![]() ,结论皆成立.
,结论皆成立.
欲使等号成立,由证明过程,知要么![]() 为一位数;要么在
为一位数;要么在![]() 的位数大于或等于2时,由式②,必须
的位数大于或等于2时,由式②,必须![]() ,此时,由式①得
,此时,由式①得![]() ,
,
即![]() 可表示为
可表示为![]() 的形式.
的形式.
上述条件也是充分的,当![]() 能够表成以上形式时,有
能够表成以上形式时,有![]() ,其余
,其余![]() .
.
故![]()


 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:高中数学 来源: 题型:
【题目】学习了余弦定理后,老师布置了一个课外任务,让同学们自己制作一些直角三角形、锐角三角形或钝角三角形的模型,现在李明和王强同学已经有了两根长度分别为![]() 和
和![]() 的铁丝.
的铁丝.
(1)如果他们希望能够制作一个直角三角形,那么他们需要的第三根铁丝的长度应该是多少?
(2)如果他们希望能够制作一个钝角三角形,那么他们需要的第三根铁丝的长度应该在什么范围?制作一个锐角三角形呢?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的焦距为2,过短轴的一个端点与两个焦点的圆的面积为
的焦距为2,过短轴的一个端点与两个焦点的圆的面积为![]() ,过椭圆
,过椭圆![]() 的右焦点作斜率为
的右焦点作斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,线段
两点,线段![]() 的中点为
的中点为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过点![]() 垂直于
垂直于![]() 的直线与
的直线与![]() 轴交于点
轴交于点![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
, ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为侧棱
为侧棱![]() 上一点.
上一点.

(1)若![]() ,求证:
,求证:![]()
![]() 平面
平面![]() ;
;
(2)求证:平面![]() 平面
平面![]() ;
;
(3)在侧棱![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ? 若存在,求出线段
? 若存在,求出线段![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地海军航空实验班面向全省遴选学员,有![]() 名初中毕业生踊跃报名投身国防,经过文化考试、体格测试、政治考核、心理选拔等过程筛选,最终招收
名初中毕业生踊跃报名投身国防,经过文化考试、体格测试、政治考核、心理选拔等过程筛选,最终招收![]() 名学员。培养学校在关注学员的文化素养同时注重学员的身体素质,要求每月至少参加一次野营拉练活动(下面简称“活动”)并记录成绩.
名学员。培养学校在关注学员的文化素养同时注重学员的身体素质,要求每月至少参加一次野营拉练活动(下面简称“活动”)并记录成绩.![]() 月某次活动中海航班学员成绩统计如图所示:
月某次活动中海航班学员成绩统计如图所示:

(1)根据图表,试估算学员在活动中取得成绩的中位数(精确到![]() );
);
(2)根据成绩从![]() 、
、![]() 两组学员中任意选出两人为一组,若选出成绩分差大于
两组学员中任意选出两人为一组,若选出成绩分差大于![]() ,则称该组为“帮扶组”,试求选出两人为“帮扶组”的概率.
,则称该组为“帮扶组”,试求选出两人为“帮扶组”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线C:y=
中,曲线C:y=![]() 与直线
与直线![]() (
(![]() >0)交与M,N两点,
>0)交与M,N两点,
(Ⅰ)当k=0时,分别求C在点M和N处的切线方程;
(Ⅱ)y轴上是否存在点P,使得当k变动时,总有∠OPM=∠OPN?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在矩形区域ABCD的A,C两点处各有一个通信基站,假设其信号覆盖范围分别是扇形区域ADE和扇形区域CBF(该矩形区域内无其他信号来源,基站工作正常).若在该矩形区域内随机地选一地点,则该地点无信号的概率是 _________ .

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且过点
,且过点![]() .
.
(1)求椭圆E的标准方程;
(2)问:是否存在过点![]() 的直线l,使以直线l被椭圆E所截得的弦
的直线l,使以直线l被椭圆E所截得的弦![]() 为直径的圆过点
为直径的圆过点![]() ,若存在,求出直线l的方程;若不存在,请说明理由.
,若存在,求出直线l的方程;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com