【题目】已知椭圆
的焦距为2，过短轴的一个端点与两个焦点的圆的面积为
，过椭圆
的右焦点作斜率为
的直线
与椭圆相交于
两点，线段
的中点为
.
(1)求椭圆的标准方程；
(2)过点垂直于的直线与
轴交于点
，且
，求
的值.
名校课堂系列答案科目：高中数学 来源： 题型：
【题目】已知椭圆的中心在原点，一个长轴端点为
，离心率
，过P分别作斜率为
的直线PA，PB，交椭圆于点A，B。
（1）求椭圆的方程；
（2）若
，则直线AB是否经过某一定点？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设函数f(x)＝|x＋2|＋|x－2|，x∈R，不等式f(x)≤6的解集为M.
（1）求M；
（2）当a2，b2∈M时，证明： 
|a＋b|≤|ab＋3|.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知等差数列{an}满足：a3＝7，a5+a7＝26，{an}的前n项和为Sn．
（1）求an及Sn；
（2）令bn＝
（n∈N*），求数列{bn}的前n项和Tn．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】通常用
、
、
分别表示
的三个内角
、
、
所对的边长，
表示的外接圆半径.
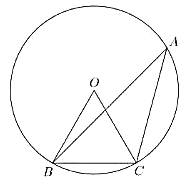
（1）如图，在以
为圆心，半径为
的圆中，
、
是圆的弦，其中
，
，角是锐角，求弦的长；
（2）在中，若
是钝角，求证：
；
（3）给定三个正实数、、，其中
，问、、满足怎样的关系时，以、为边长，为外接圆半径的不存在、存在一个或存在两个（全等的三角形算作同一个）？在存在的情况下，用、、表示.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】2016年“双节”期间，高速公路车辆较多．某调查公司在一服务区从七座以下小型汽车中按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查，将他们在某段高速公路的车速
分成六段： 
， 
， 
， 
， 
， 
后得到如图的频率分布直方图．
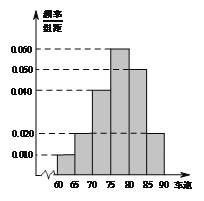
（I）某调查公司在采样中，用到的是什么抽样方法？
（II）求这40辆小型车辆车速的众数、中位数及平均数的估计值；
(III)若从车速在
的车辆中任抽取2辆，求车速在
的车辆至少有一辆的概率．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某学校为进行“阳光运动一小时”活动，计划在一块直角三角形
的空地上修建一个占地面积为
（平方米）的矩形
健身场地。如图，点
在
上，点
在
上，且
点在斜边
上，已知
米，
米，
，设矩形健身场地每平方米的造价为
元，再把矩形以外（阴影部分）铺上草坪，每平方米的造价为
元（
为正的常数）.
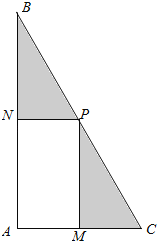
（1）试用
表示，并指出如何设计矩形的长和宽，才能使得矩形的面积最大，且求出的最大值；
（2）求总造价
关于面积的函数
，说明如何选取
，使总造价最低（不要求求出最低造价）.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】一盒中装有9张各写有一个数字的卡片，其中4张卡片上的数字是1，3张卡片上的数字是2，2张卡片上的数字是3，从盒中任取3张卡片．
（Ⅰ）求所取3张卡片上的数字完全相同的概率；
（Ⅱ）
表示所取3张卡片上的数字的中位数，求
的分布列与数学期望．
（注：若三个数
满足
，则称
为这三个数的中位数）．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
