
���� ��1���������G��ͼ���������������������㣬���ô���ϵ�����������������ԲC��һ�㷽�̣�
��2���ɣ�1���ɵ�C��-$\frac{1}{2}a$��$\frac{1}{2}��2-{a}^{2}��$������ȥa����Բ��C�������ߵĹ켣���̣�
��3����x=0���õ�ԲC��y�ύ�ڵ㣨0��0������0��2�����ɴ������N��0��$\frac{3}{2}$��������ԲC����һ��P������$\frac{|PN|}{|PM|}$Ϊһ�������ٽ���֤�����ɣ�
��� �⣺��1����x=0����������y��Ľ����ǣ�0��-a2����
��y=0����$\frac{{x}^{2}}{2}$+$\frac{a}{2}$x-a2=0�����x=-2a��x=a��
��������x��Ľ����ǣ�-2a��0������a��0����
��Բ��һ�㷽��Ϊx2+y2+Dx+Ey+F=0����$\left\{\begin{array}{l}{{a}^{4}-E{a}^{2}+F=0}\\{{a}^{2}+Da+F=0}\\{4{a}^{2}-2Da+F=0}\end{array}\right.$��
���D=a��E=a2-2��F=-2a2��
��Բ��һ�㷽��Ϊx2+y2+ax+��a2-2��y-2a2=0��
��2���ɣ�1���ɵ�C��-$\frac{1}{2}a$��$\frac{1}{2}��2-{a}^{2}��$��
��C��x��y������x=-$\frac{1}{2}a$��y=$\frac{1}{2}��2-{a}^{2}��$����ȥa���õ�y=1-2x2��
��a��0��
��x��0��
��Բ��C�������ߵĹ켣����Ϊy=1-2x2��x��0����
��3����a=0��ԲC�ķ���Ϊx2+��y-1��2=1��
��x=0���õ�ԲC��y�ύ�ڵ㣨0��0������0��2��
��������y���ϵĵ�N��0��t����t��3����
��P��ԲC�Ľ���Ϊ��0��2��ʱ��$\frac{|PN|}{|PM|}$=$\frac{|t-2|}{1}$��
��P��ԲC�Ľ���Ϊ��0��0��ʱ��$\frac{|PN|}{|PM|}$=$\frac{|t|}{3}$��
�����⣬$\frac{|t-2|}{1}$=$\frac{|t|}{3}$����t=$\frac{3}{2}$��t=3��ȥ��
����֤����N��0��$\frac{3}{2}$��������ԲC����һ��P������$\frac{|PN|}{|PM|}$Ϊһ����
��P��x��y������x2+��y-1��2=1��
��$\frac{|PN{|}^{2}}{|PM{|}^{2}}$=$\frac{{x}^{2}+��y-\frac{3}{2}��^{2}}{{x}^{2}+��y-3��^{2}}$=$\frac{1}{4}$��
��$\frac{|PN|}{|PM|}$=$\frac{1}{2}$��
����y���ϴ��ڶ���N��0��$\frac{3}{2}$�������㣺����ԲC����һ��P������$\frac{|PN|}{|PM|}$Ϊһ����$\frac{1}{2}$��
���� ���⿼��Բ�ķ��̣�����Բ�Ĺ켣���̣���������������̽��������ѧ���ļ��������������е��⣮


 һ��һ����ʱ���ϵ�д�
һ��һ����ʱ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | {1} | B�� | {0��2��3} | C�� | {0��1��2��3} | D�� | {1��2��3} |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 64 | B�� | 31 | C�� | 30 | D�� | 15 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{\sqrt{3}}{3}$ | B�� | $\sqrt{3}$ | C�� | -$\sqrt{3}$ | D�� | -$\frac{\sqrt{3}}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 һ���ռ伸���������ͼ��ͼ��ʾ��������ռ伸��������ж��㶼��ͬһ�������ϣ��������������$\frac{32}{3}$�У�
һ���ռ伸���������ͼ��ͼ��ʾ��������ռ伸��������ж��㶼��ͬһ�������ϣ��������������$\frac{32}{3}$�У��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
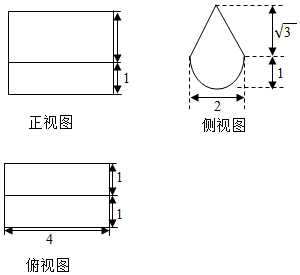 ij�����������ͼ��ͼ��ʾ�����в���ͼ���°벿������Ϊ��Բ������ü�����ı����Ϊ$5��+16+2\sqrt{3}$��
ij�����������ͼ��ͼ��ʾ�����в���ͼ���°벿������Ϊ��Բ������ü�����ı����Ϊ$5��+16+2\sqrt{3}$���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com