练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

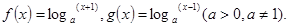    已知设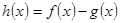
    （1）求函数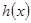的定义域；
    （2）判断函数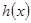的奇偶性，并予以证明；

    (1)  (2) 为奇数。

    解析试题分析：解：（1）
    ，
    则有
    即，
    则
    故的定义域6分
    (2) ,故为奇数。
    13分
    考点：函数定义域，函数的奇偶性
    点评：本试题考查了函数的基本性质的运用，结合定义分别加以说明，并理解多项式的定义域是各个定义域的交集，基础题。

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    已知函数，在时取得极值．
    （Ⅰ）求函数的解析式；
    （Ⅱ）若时,恒成立，求实数m的取值范围；
    （Ⅲ）若，是否存在实数b，使得方程在区间上恰有两个相异实数根，若存在，求出b的范围，若不存在说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    （本小题满分12分）
    已知函数，
    （1）当时，求的最大值和最小值
    （2）若在上是单调函数，且，求的取值范围

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    （本小题12分）已知函数是幂函数且在上为减函数，函数在区间上的最大值为2，试求实数的值。

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    （本小题满分12分）设计一副宣传画，要求画面积为4840，画面的宽与高的比为，画面的上，下各留8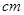空白，左右各留5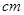空白，怎样确定画面的高于宽尺寸，能使宣传画所用纸张面积最小？

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    列车提速可以提高铁路运输量．列车运行时，前后两车必须要保持一个“安全间隔距离d（千米）”，“安全间隔距离d（千米）”与列车的速度v（千米/小时）的平方成正比（比例系数k=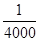）．假设所有的列车长度l均为0．4千米，最大速度均为v0（千米/小时）．问：列车车速多大时，单位时间流量Q= 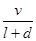最大？

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知区间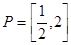，函数的定义域为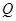
    (1)若函数在区间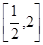上是增函数，求实数的取值范围
    （2）若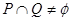，求实数的取值范围
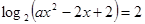    （3）若关于的方程在区间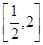内有解，求实数的取值范围

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    (本小题满分12分)
    已知函数.
    （Ⅰ）若为偶函数，求的值；
    （Ⅱ）若在上有最小值9，求的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    (满分12分)
    某市居民生活用水标准如下：

    用水量t（单位：吨）
    		每吨收费标准（单位：元）
    不超过2吨部分
    		m
    超过2吨不超过4吨部分
    		3
    超过4吨部分
    		n
    已知某用户1月份用水量为3.5吨，缴纳水费为7.5元；2月份用水量为6吨，缴纳水费为21元.设用户每月缴纳的水费为y元.
    (1)写出y关于t的函数关系式；
    (2)某用户希望4月份缴纳的水费不超过18元，求该用户最多可以用多少吨水？

    查看答案和解析>>

    同步练习册答案