（本小题满分12分）
已知函数
，
（1）当
时，求
的最大值和最小值
（2）若在上是单调函数，且
，求
的取值范围
阅读快车系列答案科目：高中数学 来源： 题型：解答题
某单位用2160万元购得一块空地，计划在该地块上建造一栋至少10层、每层2000平方米的楼房．经测算，如果将楼房建为
层，则每平方米的平均建筑费用为
（单位：元）．为了使楼房每平方米的平均综合费用最少，该楼房应建为多少层？
（注：平均综合费用
平均建筑费用
平均购地费用，平均购地费用
）
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
在边长为60cm的正方形铁皮的四角切去相等的正方形，再把它的边沿虚线折起（如图），做成一个无盖的方底箱子，箱底边长为多少时，箱子容积最大？最大容积是多少？
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
一家报刊推销员从报社买进报纸的价格是每份0.20元，卖出的价格是每份0.30元，卖不完的还可以以每份0.08元的价格退回报社．在一个月（以30天计算）有20天每天可卖出400份，其余10天只能卖250份，但每天从报社买进报纸的份数都相同，问应该从报社买多少份才能使每月所获得的利润最大？并计算每月最多能赚多少钱？
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
（本小题满分12分）
统计表明，某种型号的汽车在匀速行驶中每小时耗油量y（升）关于行驶速度x（千米/小时）的函数解析式可以表示为：
.已知甲、乙两地相距100千米。
（1）当汽车以40千米/小时的速度匀速行驶时，从甲地到乙地要耗油多少升？
（2）当汽车以多大的速度匀速行驶时，从甲地到乙地耗油最少？最少为多少升？
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
(本题满分16分)
如图，开发商欲对边长为
的正方形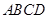
地段进行市场开发，拟在该地段的一角建设一个景观，需要建一条道路
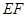（点
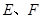分别在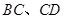
上），根据规划要求
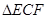的周长为
．
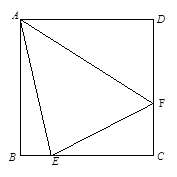
（1）设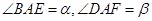
，求证：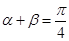
；
（2）欲使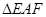
的面积最小，试确定点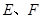的位置．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
，函数
;（2）
时，
在
上单调递减，在
上单调递增
当
时，函数
时，函数
或
或
，又
且关于
的方程
在
上有两个不相等的实数根.⑴求
的解析式.⑵若
总有
成立，求
的最大值.
对一切实数x恒成立，求实数a的取值范围。
在区间
上的最小值
的表达式。
设
的定义域；