
(本小题满分12分)
统计表明,某种型号的汽车在匀速行驶中每小时耗油量y(升)关于行驶速度x(千米/小时)的函数解析式可以表示为: .已知甲、乙两地相距100千米。
.已知甲、乙两地相距100千米。
(1)当汽车以40千米/小时的速度匀速行驶时,从甲地到乙地要耗油多少升?
(2)当汽车以多大的速度匀速行驶时,从甲地到乙地耗油最少?最少为多少升?
(1) 当汽车以40千米/小时的速度匀速行驶时,从甲地到乙地耗油17.5升.
(2) 当汽车以80千米/小时的速度匀速行驶时,从甲地到乙地耗油最少,最少为11.25升.
解析试题分析:(1)当x=40时,汽车从甲地到乙地行驶了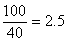 小时,
小时,
要耗油(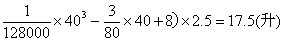 .
.
答:当汽车以40千米/小时的速度匀速行驶时,从甲地到乙地耗油17.5升.
(2)当速度为x千米/小时,汽车从甲地到乙地行驶了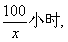 设耗油量为h(x)升,依题意得h (x)=(
设耗油量为h(x)升,依题意得h (x)=(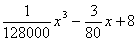 )·
)·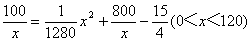 ,
,
h’(x)=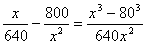 (0<x≤120)
(0<x≤120)
令h’(x)=0,得x=80.
当x∈(0,80)时,h’(x)<0,h(x)是减函数;
当x∈(80,120)时,h’(x)>0,h(x)是增函数.
∴当x=80时,h(x)取到极小值h(80)=11.25.
因为h(x)在(0,120)上只有一个极值,所以它是最小值.
答:当汽车以80千米/小时的速度匀速行驶时,从甲地到乙地耗油最少,最少为11.25升.
考点:函数模型的运用
点评:解决的关键是理解导数的几何意义,以及运用导数来求解函数的单调性得到最值,属于基础题。


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
建造一断面为等腰梯形的防洪堤(如图),梯形的腰与底边所角为60°,考虑到防洪堤坚固性及石块用料等因素,设计其断面面积为 m2,为了使堤的上面与两侧面的水泥用料最省,要求断面的外周长(梯形的上底BC与两腰长的和)最小.如何设计防洪堤,才能使水泥用料最省.
m2,为了使堤的上面与两侧面的水泥用料最省,要求断面的外周长(梯形的上底BC与两腰长的和)最小.如何设计防洪堤,才能使水泥用料最省.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某商店经销一种奥运会纪念品,每件产品的成本为30元,并且每卖出一件产品需向税务部门上交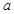 元(
元(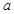 为常数,2≤a≤5 )的税收。设每件产品的售价为x元(35≤x≤41),根据市场调查,日销售量与
为常数,2≤a≤5 )的税收。设每件产品的售价为x元(35≤x≤41),根据市场调查,日销售量与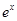 (e为自然对数的底数)成反比例。已知每件产品的日售价为40元时,日销售量为10件。
(e为自然对数的底数)成反比例。已知每件产品的日售价为40元时,日销售量为10件。
(1)求该商店的日利润L(x)元与每件产品的日售价x元的函数关系式;
(2)当每件产品的日售价为多少元时,该商品的日利润L(x)最大,并求出L(x)的最大值。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
列车提速可以提高铁路运输量.列车运行时,前后两车必须要保持一个“安全间隔距离d(千米)”,“安全间隔距离d(千米)”与列车的速度v(千米/小时)的平方成正比(比例系数k=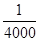 ).假设所有的列车长度l均为0.4千米,最大速度均为v0(千米/小时).问:列车车速多大时,单位时间流量Q=
).假设所有的列车长度l均为0.4千米,最大速度均为v0(千米/小时).问:列车车速多大时,单位时间流量Q=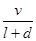 最大?
最大?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分12分)通常情况下,同一地区一天的温度随时间变化的曲线接近于函数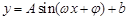 的图像.2013年1月下旬荆门地区连续几天最高温度都出现在14时,最高温度为
的图像.2013年1月下旬荆门地区连续几天最高温度都出现在14时,最高温度为 ;最低温度出现在凌晨2时,最低温度为零下
;最低温度出现在凌晨2时,最低温度为零下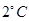 .
.
(Ⅰ)请推理荆门地区该时段的温度函数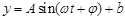
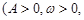
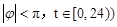 的表达式;
的表达式;
(Ⅱ)29日上午9时某高中将举行期末考试,如果温度低于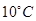 ,教室就要开空调,请问届时学校后勤应该送电吗?
,教室就要开空调,请问届时学校后勤应该送电吗?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com