
分析 (1)计算所有事件数已经满足条件的事件数,利用古典概型公式求之;
(2)设两人到达的时间分别为9点到10点之间的x分钟、y分钟.用(x,y)表示每次试验的结果,分别,x,y范围表示满足条件的事件,利用几何概型的概率公式得到所求.
解答 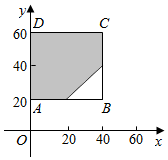 解:(1)从袋中8个球中有放回的摸出2个,试验的结果共有8×8=64(种)中奖的情况分为两种:
解:(1)从袋中8个球中有放回的摸出2个,试验的结果共有8×8=64(种)中奖的情况分为两种:
(i)2个球都是红色,包含的基本事件数为5×5=25;
(ii)2个球都是白色,包含的基本事件数为3×3=9.
所以,中奖这个事件包含的基本事件数为25+9=34.
因此,中奖概率为$\frac{34}{64}=\frac{17}{32}$.…(6分)
(2)设两人到达的时间分别为9点到10点之间的x分钟、y分钟.
用(x,y)表示每次试验的结果,则所有可能结果为Ω={(x,y)|0≤x≤40,20≤y≤60};
记甲比乙提前到达为事件A,则事件A的可能结果为A={(x,y)|x<y,0≤x≤40,20≤y≤60}.
如图所示,试验全部结果构成区域Ω为正方形ABCD.而事件A所构成区域是正方形内的阴影部分.
根据几何概型公式,得到P(A)=$\frac{{S}_{阴影}}{{S}_{正方形}}=\frac{4{0}^{2}-\frac{1}{2}×2{0}^{2}}{4{0}^{2}}=\frac{7}{8}$.
所以,甲比乙提前到达的概率为$\frac{7}{8}$.…(12分)
点评 本题考查了古典概型和几何概型的概率求法;关键字明确事件的表达方式,利用相关的公式解答.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
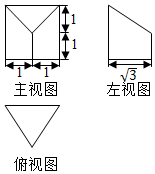
| A. | 2$\sqrt{3}$ | B. | $\frac{5\sqrt{3}}{3}$ | C. | $\frac{4\sqrt{3}}{3}$ | D. | $\frac{2\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
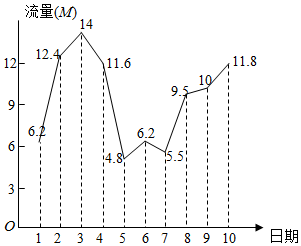 小王的手机使用的是每月300M流量套餐,如图记录了小王在4月1日至4月10日这十天的流量使用情况,下列叙述中正确的是( )
小王的手机使用的是每月300M流量套餐,如图记录了小王在4月1日至4月10日这十天的流量使用情况,下列叙述中正确的是( )| A. | 1日-10日这10天的平均流量小于9.0M/日 | |
| B. | 11日-30日这20天,如果每天的平均流量不超过11M,这个月总流量就不会超过套餐流量 | |
| C. | 从1日-10日这10天的流量中任选连续3天的流量,则3日,4日,5日这三天的流量的方差最大 | |
| D. | 从1日-10日这10天中的流量中任选连续3天的流量,则8日,9日,10日这三天的流量的方差最小 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{12}{25}$ | B. | $\frac{24}{25}$ | C. | -$\frac{24}{25}$ | D. | -$\frac{12}{25}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1+$\frac{1}{e}$,e] | B. | [1+$\frac{1}{e}$,e] | C. | (1,e] | D. | (2+$\frac{1}{e}$,e] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com